Kinetic momentum
Encyclopedia
In physics, in particular electromagnetism, the kinetic momentum is a nonstandard term for the momentum of a charged particle due to its inertia. When a charged particle interacts with an electromagnetic field
(often abbreviated as EM field), there are two momenta: due to its inertia and due to the field. It is distinguished from the canonical momentum, because the kinetic momentum includes a contribution from the vector potential
.
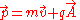
where the momenta are:
furthermore:
The motivations for these names are as follows. An EM field possesses energy and momentum, a particle has charge. Charged particles interact with electromagnetic fields due to the electromagnetic interaction. So the momentum in the field is gained by the particle when it interacts with it. This contribution due to the field presents itself in terms of the particle's charge and the A-field. The particle also has mass and is moving with velocity, which is the familiar form of momentum as a quantity of motion, hence the term kinetic momentum. The total momentum possessed by the particle is the vector sum of these momenta: the canonical momentum.
for a particle in interaction with an electromagnetic field
is:
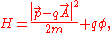
where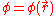
is the scalar potential
.
The Hamiltonian
H is an expression for the total energy as a sum of the kinetic energy
T and the potential energy
V:
The kinetic energy always corresponds to the kinetic momentum:
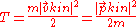
which is a familiar relation from classical mechanics
. For electrodynamics,
substituting to get the kinetic energy of the charged particle:
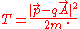
The potential energy is simply the potential times the charge (since electric potential
is defined as potential energy per unit charge):
, the Lagrangian
for the particle interacting with the field is
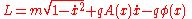
The action is the relativistic arclength of the path of the particle in space time, minus the potential energy contribution, plus an extra contribution which quantum mechanically
is an extra phase a charged particle gets when it is moving along a vector potential.
The momentum conjugate to x, that is the canonical momentum p, is defined from the variation of the lagrangian:
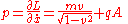
The kinetic momentum is the relativistic momentum of a particle moving with velocity v, still (p – qA), so we have: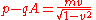
The Hamiltonian equals total energy (kinetic plus potential), and is the usual relativistic expression for the energy. So in terms of the kinetic momentum: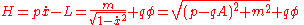
The equations of motion derived by extremizing
the action:
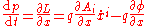
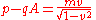
are the same as Hamilton's equations of motion
:
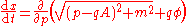
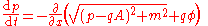
both are equivalent to the noncanonical form:
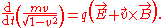
This formula represents the rate at which the Lorentz force
adds relativistic momentum to the particle.
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
(often abbreviated as EM field), there are two momenta: due to its inertia and due to the field. It is distinguished from the canonical momentum, because the kinetic momentum includes a contribution from the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
.
Definition and terminology
The momenta associated with a charged particle in an electromagnetic field is: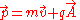where the momenta are:
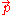is the canonical momentum,
is the kinetic momentum,
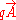is the potential momentum,
furthermore:
- q = charge of particle,
- m = mass,
is the velocity of the charge,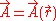
is the magnetic vector potential; aka the A-field,
The motivations for these names are as follows. An EM field possesses energy and momentum, a particle has charge. Charged particles interact with electromagnetic fields due to the electromagnetic interaction. So the momentum in the field is gained by the particle when it interacts with it. This contribution due to the field presents itself in terms of the particle's charge and the A-field. The particle also has mass and is moving with velocity, which is the familiar form of momentum as a quantity of motion, hence the term kinetic momentum. The total momentum possessed by the particle is the vector sum of these momenta: the canonical momentum.
Non-relativistic dynamics
The non-relativistic HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
for a particle in interaction with an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
is:
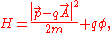
where
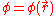is the scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
.
The Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
H is an expression for the total energy as a sum of the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
T and the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
V:
The kinetic energy always corresponds to the kinetic momentum:
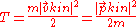
which is a familiar relation from classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. For electrodynamics,
substituting to get the kinetic energy of the charged particle:
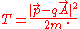
The potential energy is simply the potential times the charge (since electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
is defined as potential energy per unit charge):
Relativistic dynamics
In relativityTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
for the particle interacting with the field is
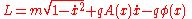
The action is the relativistic arclength of the path of the particle in space time, minus the potential energy contribution, plus an extra contribution which quantum mechanically
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is an extra phase a charged particle gets when it is moving along a vector potential.
The momentum conjugate to x, that is the canonical momentum p, is defined from the variation of the lagrangian:
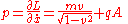
The kinetic momentum is the relativistic momentum of a particle moving with velocity v, still (p – qA), so we have:
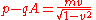
The Hamiltonian equals total energy (kinetic plus potential), and is the usual relativistic expression for the energy. So in terms of the kinetic momentum:
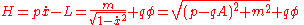
The equations of motion derived by extremizing
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
the action:
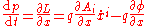
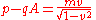
are the same as Hamilton's equations of motion
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
:
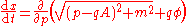
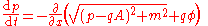
both are equivalent to the noncanonical form:
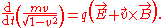
This formula represents the rate at which the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
adds relativistic momentum to the particle.
Sources
- Classical Mechanics (2nd Edition), T.W.B. Kibble, European Physics Series, Mc Graw Hill (UK), 1973, ISBN 07-084018-0. Although concentrates on undergraduate-level classical Newtonian and Lagrangian mechanics, also contains a chapter on potential theory, includes electrodynamic fields: the ϕ and A fields and canonical momentum.
- Quantum mechanics, E. Abers, 2003, Benjamin-Cummings Publishers, ISBN(10) 0-1314-6100-1. Focuses on graduate-level quantum mechanics, but also contains simalar coverage to the above.
- Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN 978-0-07-154382-8. Again concentrates on under/post-graduate level quantum mechanics, but does provide some exposure to lagrangian field theory and application to the EM field.