Kinetic scheme
Encyclopedia
In physics
and chemistry
and related fields, a kinetic scheme is a network of states and connections among the states representing the scheme of a dynamical process. Usually, a kinetic scheme represents a Markovian process, where when the process is not Markovian, the scheme is a generalized kinetic scheme. See Fig. 1 for an illustration of a kinetic scheme.
is directional and connects states i with j. Indeed, when detailed balance
exists in a system, the following relation holds,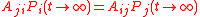
, for every connected states i and j. (The result represents the fact that any closed loop in a Markovian network in equilibrium does not have a net flow.)
: a first-order differential equation
for the probability
of a system to occupy each one its states at time t; written in a matrix form, we see: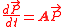
, where 
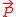is a column vector (where element i represents state i), and 
is the matrix of connections. In a Markovian kinetic scheme the connections are simply numbers (and any jumping time probability density function for state i is an exponential, with a rate equal the value of all the exiting connections).
Matrix
can also represent birth and death, meaning that probability is injected (birth) or taken from (death) the system, where then, the process is not in equilibrium. (These terms are different than a birth-death process
, where there we have simply a linear kinetic scheme).
An example for such a process is a reduced dimensions form
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
and related fields, a kinetic scheme is a network of states and connections among the states representing the scheme of a dynamical process. Usually, a kinetic scheme represents a Markovian process, where when the process is not Markovian, the scheme is a generalized kinetic scheme. See Fig. 1 for an illustration of a kinetic scheme.
Description of the form of a kinetic scheme
A kinetic scheme is a network of states. Each state is special, usually, has a special number, representing a specific state in the system (although repetitions of states may occur and this depends on the system). Each pair of connected states has at least one rate; a rate is directional and connects states i with j. Indeed, when detailed balanceDetailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
exists in a system, the following relation holds,
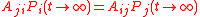, for every connected states i and j. (The result represents the fact that any closed loop in a Markovian network in equilibrium does not have a net flow.)Mathematical description
The kinetic scheme is described with a master equationMaster equation
In physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
: a first-order differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
for the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of a system to occupy each one its states at time t; written in a matrix form, we see:
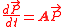, where 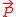is a column vector (where element i represents state i), and is the matrix of connections. In a Markovian kinetic scheme the connections are simply numbers (and any jumping time probability density function for state i is an exponential, with a rate equal the value of all the exiting connections).Matrix
can also represent birth and death, meaning that probability is injected (birth) or taken from (death) the system, where then, the process is not in equilibrium. (These terms are different than a birth-death processBirth-death process
The birth–death process is a special case of continuous-time Markov process where the states represent the current size of a population and where the transitions are limited to births and deaths...
, where there we have simply a linear kinetic scheme).
Specific Markovian kinetic schemes
- A birth-death processBirth-death processThe birth–death process is a special case of continuous-time Markov process where the states represent the current size of a population and where the transitions are limited to births and deaths...
is a linear one-dimensional Markovian kinetic scheme. - Michaelis–Menten kinetics are a type of a Markovian kinetic scheme when solved with the steady state assumption for the creation of intermediates in the reaction pathway.
Generalizations of Markovian kinetic schemes
- A kinetic scheme with time dependent rates: When the connections depend on the actual time (i.e. matrix
depends on the time,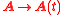 
), the process is not Markovian, and the master equation obeys, 
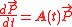. The reason for a time dependent rates is, for example, a time dependent external field applied on a Markovian kinetic scheme (thus making the process a not Markovian one). - A semi-Markovian kinetic scheme: When the connections represent multi exponential jumping time probability density functions, the process is semi-MarkovianSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...
, and the equation of motion is an integro-differential equationIntegro-differential equationAn integro-differential equation is an equation which involves both integrals and derivatives of a function.The general first-order, linear integro-differential equation is of the form...
termed the generalized master equation: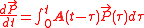
.
An example for such a process is a reduced dimensions form
Reduced dimensions form
In biophysics and related fields, reduced dimension forms are unique on-off mechanisms for random walks that generate two-state trajectories...
.
- The Fokker Planck equation: when expanding the master equation of the kinetic scheme in a continuous space coordinate, one finds the Fokker Planck equation.
See also
- Markov processMarkov processIn probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
- Continuous-time Markov process
- Master equationMaster equationIn physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
- Detailed balanceDetailed balanceThe principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
- Graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
- Semi-Markov processSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...