
Kirchhoff's diffraction formula
Encyclopedia
Kirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling
. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen. The equation is derived by making several approximations to the Kirchhoff integral theorem
which uses Green's theorem
to derive the solution to the homogeneous wave equation
.
, sometimes referred to as the Fresnel-Kirchhoff integral theorem, uses Green's theorem
to derive the solution to the homogeneous wave equation
at an arbitrary point P in terms of the values of the solution of the wave equation and its first order derivative at all points on an arbitrary surface which encloses P.
The solution provided by the integral theorem for a monochromatic source is:
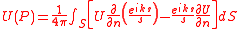
where is the complex amplitude of the disturbance at the surface, is the wavenumber
and is the distance from P to the surface.
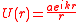
where represents the magnitude of the disturbance at the point source.
The disturbance at a point P can be found by applying the integral theorem to the closed surface which is formed by the intersection of a sphere of radius R with the screen. The integration is performed over the areas , and giving
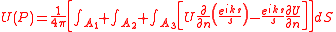
To solve the equation, it is assumed that the values of and in the area are the same as when the screen is not present, giving:
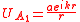
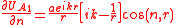
at P0, is the length P0Q, and (n,r) is the angle between P0Q and the normal to the aperture.
Kirchoff assumes that the values of and in are zero. This implies that and are discontinuous at the edge of the aperture. This is not the case, and this is one of the approximation used in deriving the equation. These assumptions are sometimes referred to as Kirchhoff's boundary conditions.
The contribution from A3 to the integral is also assumed to be zero. This can be justified by making the assumption that the source starts to radiate at a particular time, and then by making R large enough, so that when the disturbance at P is being considered, no contributions from A3 will have arrived there. Such a wave is no longer monochromatic, since a monochromatic wave must exist at all times, but that assumption is not necessary, and a more formal argument avoiding its use has been derived.
We have

where is the angle between the normal to the aperture and QP.
Finally, the terms and are assumed to be negligible compared with , since and are generally much greater than which is equal to the wavelength
. Thus, the integral above, which represents the complex amplitude at P, becomes:

This is the Kirchhoff or Fresnel–Kirchhoff diffraction formula.
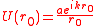
The diffraction formula becomes;
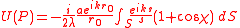
This is the Kirchhoff's diffraction formula which contains parameters which had to be arbitrarily assigned in the derivation of the Huygens–Fresnel equation.
It is assumed, as before, that the values of and in the area are the same as when the screen is not present, that the values of and in are zero (Kirchhoff's boundary conditions) and that the contribution from A3 to the integral are also zero. It is also assumed that is negligible compared with . We then have
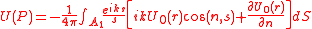
This is the most general form of the Kirchhoff diffraction formula. To solve this equation for an extended source, an additional integration would be required to sum the contributions made by the individual points in the source. If, however, we assume that the light from the source at each point in the aperture has a well-defined direction, which is the case of the distance between the source and the aperture is significantly greater than the wavelength, then we can write

where is the magnitude of the disturbance at the point in the aperture. We then have:
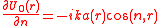
We then have:

equation and Fraunhofer diffraction
equation, which are approximations of Kirchhoff's formula for the near field and far field, can be applied to a very wide range of optical systems.
One of the important assumptions made in arriving at the Kirchhoff diffraction formula is that are significantly greater than λ. A further approximation can be made which significantly simplifies the equation further: this is that the distances P0Q and QP are much greater than the dimensions of the aperture. This allows one to make two further approximations:
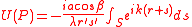
We assume that the aperture lies in the plane, and the co-ordinates of P0, P and Q (a general point in the aperture) are , and respectively. We then have:


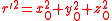
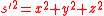
We can express and as follows:


These can be expanded as power series:
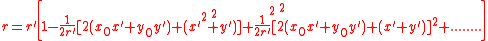
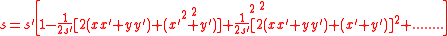
The complex amplitude at P can now be expressed as:
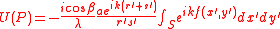
where includes all the terms in the expressions above for and apart from the first term in each expression and can be written in the form:
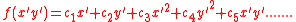
where the are constants.
diffraction equation. If the direction cosines of P0Q and PQ are
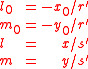
the Fraunhofer diffraction equation is then
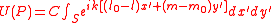
where is a constant. This can also be written in the form:
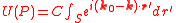
where and are the wave vector
s of the waves travelling from P0 to the aperture and from the aperture to P respectively, and r' is a point in the aperture.
If the point source is replaced by an extended source whose complex amplitude at the aperture is given by then the Fraunhofer diffraction
equation is: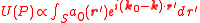
where is, as before, the magnitude of the disturbance at the aperture.
equation.
are significantly greater than the size of the aperture
are significantly greater than the size of the aperture
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen. The equation is derived by making several approximations to the Kirchhoff integral theorem
Kirchhoff integral theorem
Kirchhoff's theorem uses Green's theorem to derive the solution to the homogeneous wave equation at an arbitrary point P in terms of the values of the solution of the wave equation and its first order derivative at all points on an arbitrary surface which encloses P...
which uses Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
to derive the solution to the homogeneous wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
.
Derivation of Kirchhoff's diffraction formula
Kirchhoff's integral theoremKirchhoff integral theorem
Kirchhoff's theorem uses Green's theorem to derive the solution to the homogeneous wave equation at an arbitrary point P in terms of the values of the solution of the wave equation and its first order derivative at all points on an arbitrary surface which encloses P...
, sometimes referred to as the Fresnel-Kirchhoff integral theorem, uses Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
to derive the solution to the homogeneous wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
at an arbitrary point P in terms of the values of the solution of the wave equation and its first order derivative at all points on an arbitrary surface which encloses P.
The solution provided by the integral theorem for a monochromatic source is:
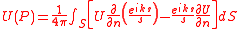
where is the complex amplitude of the disturbance at the surface, is the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
and is the distance from P to the surface.
Point source
Consider a monochromatic point source at P0 which illuminates an aperture in a screen. The energy of the wave emitted by a point source falls off as the inverse square of the distance travelled, so the amplitude falls off as the inverse of the distance. The complex amplitude of the disturbance at a distance is given by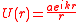
where represents the magnitude of the disturbance at the point source.
The disturbance at a point P can be found by applying the integral theorem to the closed surface which is formed by the intersection of a sphere of radius R with the screen. The integration is performed over the areas , and giving
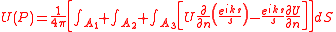
To solve the equation, it is assumed that the values of and in the area are the same as when the screen is not present, giving:
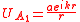
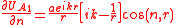
at P0, is the length P0Q, and (n,r) is the angle between P0Q and the normal to the aperture.
Kirchoff assumes that the values of and in are zero. This implies that and are discontinuous at the edge of the aperture. This is not the case, and this is one of the approximation used in deriving the equation. These assumptions are sometimes referred to as Kirchhoff's boundary conditions.
The contribution from A3 to the integral is also assumed to be zero. This can be justified by making the assumption that the source starts to radiate at a particular time, and then by making R large enough, so that when the disturbance at P is being considered, no contributions from A3 will have arrived there. Such a wave is no longer monochromatic, since a monochromatic wave must exist at all times, but that assumption is not necessary, and a more formal argument avoiding its use has been derived.
We have

where is the angle between the normal to the aperture and QP.
Finally, the terms and are assumed to be negligible compared with , since and are generally much greater than which is equal to the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. Thus, the integral above, which represents the complex amplitude at P, becomes:

This is the Kirchhoff or Fresnel–Kirchhoff diffraction formula.
Equivalence to Huygens–Fresnel equation
The Huygens–Fresnel principle can be derived by integrating over a different closed surface. The area A1 above is replaced by a wavefront from P0 which almost fills the aperture, and a portion of a cone with a vertex at P0 which is labelled A4 in the diagram. If the radius of curvature of the wave is large enough, the contribution from A4 can be neglected. We also have where is as defined in Huygens–Fresnel principle and = 1. The complex amplitude of the wavefront at is given by: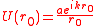
The diffraction formula becomes;
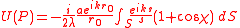
This is the Kirchhoff's diffraction formula which contains parameters which had to be arbitrarily assigned in the derivation of the Huygens–Fresnel equation.
Extended source
Assume that the aperture is illuminated by an extended source wave. The complex amplitude at the aperture is given byIt is assumed, as before, that the values of and in the area are the same as when the screen is not present, that the values of and in are zero (Kirchhoff's boundary conditions) and that the contribution from A3 to the integral are also zero. It is also assumed that is negligible compared with . We then have
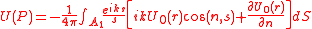
This is the most general form of the Kirchhoff diffraction formula. To solve this equation for an extended source, an additional integration would be required to sum the contributions made by the individual points in the source. If, however, we assume that the light from the source at each point in the aperture has a well-defined direction, which is the case of the distance between the source and the aperture is significantly greater than the wavelength, then we can write

where is the magnitude of the disturbance at the point in the aperture. We then have:
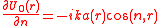
We then have:

Fraunhofer and Fresnel diffraction equations
In spite of the various approximations which were made in arriving at the formula, it is adequate to describe the majority of problems in instrumental optics. This is mainly because the wavelength of light is much smaller than the dimensions of any obstacles encountered. Analytical solutions are not possible for most configurations but the Fresnel diffractionFresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
equation and Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
equation, which are approximations of Kirchhoff's formula for the near field and far field, can be applied to a very wide range of optical systems.
One of the important assumptions made in arriving at the Kirchhoff diffraction formula is that are significantly greater than λ. A further approximation can be made which significantly simplifies the equation further: this is that the distances P0Q and QP are much greater than the dimensions of the aperture. This allows one to make two further approximations:
- is replaced with where is the angle between P0P and the normal to the aperture. The factor is replaced with where are the distances from P0 and P to the origin, which is located in the aperture. The complex amplitude then becomes:
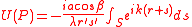
We assume that the aperture lies in the plane, and the co-ordinates of P0, P and Q (a general point in the aperture) are , and respectively. We then have:


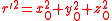
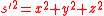
We can express and as follows:


These can be expanded as power series:
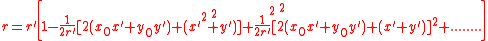
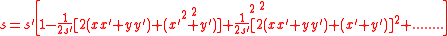
The complex amplitude at P can now be expressed as:
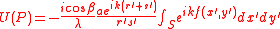
where includes all the terms in the expressions above for and apart from the first term in each expression and can be written in the form:
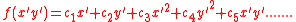
where the are constants.
Fraunhofer diffraction
If all the terms in can be neglected except for the terms in and , we have the FraunhoferFraunhofer
Fraunhofer, , may refer to:*Joseph von Fraunhofer , German physicist*Fraunhofer , a lunar crater*Fraunhofer Society , a large German research organization with 59 institutes throughout Germany...
diffraction equation. If the direction cosines of P0Q and PQ are
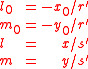
the Fraunhofer diffraction equation is then
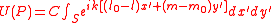
where is a constant. This can also be written in the form:
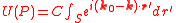
where and are the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
s of the waves travelling from P0 to the aperture and from the aperture to P respectively, and r' is a point in the aperture.
If the point source is replaced by an extended source whose complex amplitude at the aperture is given by then the Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
equation is:
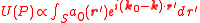
where is, as before, the magnitude of the disturbance at the aperture.
Fresnel diffraction
When the quadratic terms cannot be neglected but all higher order terms can, the equation becomes the Fresnel diffractionFresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
equation.
Assumptions made
The diffraction equation is arrived at by applying Green's theorem to the solution of the wave equation. The approximations made in deriving the Kirchhoff, Fraunhofer and Fresnel equations are summarised in the following sections.Kirchhoff diffraction equation
and are discontinuous at the boundaries of the aperture and are much greater thanFraunhofer diffraction equations
In addition to the approximations made in deriving the Kirchhoff equation, it is assumed thatare significantly greater than the size of the aperture
- Second and higher order terms in the expression can be neglected
Fresnel diffraction equation
In addition to the approximations used in deriving the Kirchhoff equation, it is assumed thatare significantly greater than the size of the aperture
- Third and higher order terms in the expression can be neglected

