
Kirchhoff integral theorem
Encyclopedia
Kirchhoff's theorem uses Green's theorem
to derive the solution to the homogeneous wave equation
at an arbitrary point P in terms of the values of the solution of the wave equation and its first order derivative at all points on an arbitrary surface which encloses P. The integral has the following form for a monochromatic wave:
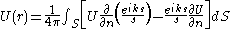
where the integration is performed over the whole of the arbitrary surface S, s is the distance between the point r and the surface S, and denotes integration along the inward normal on the surface.
A more general form can be derived for non-monochromatic waves. The complex amplitude of the wave can be represented by a Fourier integral of the form:
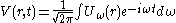
where, by Fourier inversion, we have:
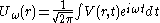
The integral theorem (above) is applied to each each Fourier component , and the following expression is obtained

where the square brackets on terms denote retarded values, i.e. the values at time .
Kirchhoff showed that equation can be approximated in many cases to a simpler form, known as the Kirchhoff, or Fresnel-Kirchhoff diffraction formula
, which is equivalent to the Huygens-Fresnel equation
, but provides a formula for the inclination factor which is not defined in the latter. The diffraction integral can be applied to a wide range of problems in optics.
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
to derive the solution to the homogeneous wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
at an arbitrary point P in terms of the values of the solution of the wave equation and its first order derivative at all points on an arbitrary surface which encloses P. The integral has the following form for a monochromatic wave:
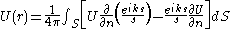
where the integration is performed over the whole of the arbitrary surface S, s is the distance between the point r and the surface S, and denotes integration along the inward normal on the surface.
A more general form can be derived for non-monochromatic waves. The complex amplitude of the wave can be represented by a Fourier integral of the form:
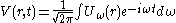
where, by Fourier inversion, we have:
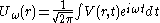
The integral theorem (above) is applied to each each Fourier component , and the following expression is obtained

where the square brackets on terms denote retarded values, i.e. the values at time .
Kirchhoff showed that equation can be approximated in many cases to a simpler form, known as the Kirchhoff, or Fresnel-Kirchhoff diffraction formula
Kirchhoff's diffraction formula
Kirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen...
, which is equivalent to the Huygens-Fresnel equation
Huygens-Fresnel principle
The Huygens–Fresnel principle is a method of analysis applied to problems of wave propagation both in the far-field limit and in near-field diffraction.-History:...
, but provides a formula for the inclination factor which is not defined in the latter. The diffraction integral can be applied to a wide range of problems in optics.

