Klee's measure problem
Encyclopedia
In computational geometry
, Klee's measure problem is the problem of determining how efficiently the measure
of a union
of (multidimensional
) rectangular ranges can be computed. Here, a d-dimensional rectangular range is defined to be a cartesian product
of d intervals
of real number
s, which is a subset
of Rd.
The problem is named after Victor Klee
, who gave an algorithm for computing the length of a union of interval
s (the case d = 1) which was later shown to be optimally efficient in the sense of computational complexity theory
. The computational complexity of computing the area of a union of 2-dimensional rectangular ranges is now also known, but the case d ≥ 3 remains an open problem
.
considered the following problem: given a collection of n intervals
in the real line
, compute the length of their union. He then presented an algorithm
to solve this problem with computational complexity
(or "running time")
— see Big O notation
for the meaning of this statement. This algorithm, based on sorting
the intervals, was later shown by Michael Fredman
and Bruce Weide (1978) to be optimal.
Later in 1977, Jon Bentley
considered a 2-dimensional analogue of this problem: given a collection of n rectangle
s, find the area of their union. He also obtained a complexity
algorithm, now known as Bentley's algorithm, based on reducing the problem to n 1-dimensional problems: this is done by sweeping a vertical line across the area. Using this method, the area of the union can be computed without explicitly constructing the union itself. Bentley's algorithm is now also known to be optimal (in the 2-dimensional case), and is used in computer graphics
, among other areas.
These two problems are the 1- and 2-dimensional cases of a more general question: given a collection of n d-dimensional rectangular ranges, compute the measure of their union. This general problem is Klee's measure problem.
When generalized to the d-dimensional case, Bentley's algorithm has a running time of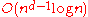
. This turns out not to be optimal, because it only decomposes the d-dimensional problem into n (d-1)-dimensional problems, and does not further decompose those subproblems. In 1981, Jan van Leeuwen
and Derek Wood improved the running time of this algorithm to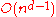
for d ≥ 3 by using dynamic quadtree
s.
In 1988, Mark Overmars
and Chee Yap proposed an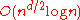
algorithm for d ≥ 3 which is the fastest known algorithm to date. Their algorithm uses a particular data structure similar to a kd-tree
to decompose the problem into 2-dimensional components and aggregate those components efficiently; the 2-dimensional problems themselves are solved efficiently using a trellis
structure. Although asymptotically faster than Bentley's algorithm, its data structures use significantly more space, so it is only used in problems where either n or d is large. In 1998, Bogdan Chlebus proposed a simpler algorithm with the same asymptotic running time for the common special cases where d is 3 or 4.
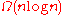. The Overmars–Yap algorithm provides an upper bound of 
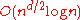, so for d ≥ 3, it remains an open question whether faster algorithms are possible, or alternatively whether tighter lower bounds can be proven. In particular, it remains open whether the algorithm's running time must depend on d. In addition, the question of whether there are faster algorithms that can deal with special cases (for example, when the input coordinates are integers within a bounded range) remains open.
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, Klee's measure problem is the problem of determining how efficiently the measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of a union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of (multidimensional
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
) rectangular ranges can be computed. Here, a d-dimensional rectangular range is defined to be a cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of d intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, which is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Rd.
The problem is named after Victor Klee
Victor Klee
Victor L. Klee, Jr. was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle.Born in San Francisco, Vic Klee earned his B.A...
, who gave an algorithm for computing the length of a union of interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
s (the case d = 1) which was later shown to be optimally efficient in the sense of computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. The computational complexity of computing the area of a union of 2-dimensional rectangular ranges is now also known, but the case d ≥ 3 remains an open problem
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
.
History and algorithms
In 1977, Victor KleeVictor Klee
Victor L. Klee, Jr. was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle.Born in San Francisco, Vic Klee earned his B.A...
considered the following problem: given a collection of n intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
in the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, compute the length of their union. He then presented an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to solve this problem with computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
(or "running time")
— see Big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
for the meaning of this statement. This algorithm, based on sorting
Sorting
Sorting is any process of arranging items in some sequence and/or in different sets, and accordingly, it has two common, yet distinct meanings:# ordering: arranging items of the same kind, class, nature, etc...
the intervals, was later shown by Michael Fredman
Michael Fredman
Michael Lawrence Fredman is a professor at the Computer Science Department at Rutgers University, United States. He got his Ph. D. degree from Stanford University in 1972 under the supervision of Donald Knuth. He was a member of the mathematics department at the Massachusetts Institute of...
and Bruce Weide (1978) to be optimal.
Later in 1977, Jon Bentley
Jon Bentley
Jon Louis Bentley is a researcher in the field of computer science. He is credited with the invention of the k-d tree....
considered a 2-dimensional analogue of this problem: given a collection of n rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s, find the area of their union. He also obtained a complexity
algorithm, now known as Bentley's algorithm, based on reducing the problem to n 1-dimensional problems: this is done by sweeping a vertical line across the area. Using this method, the area of the union can be computed without explicitly constructing the union itself. Bentley's algorithm is now also known to be optimal (in the 2-dimensional case), and is used in computer graphicsComputer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, among other areas.
These two problems are the 1- and 2-dimensional cases of a more general question: given a collection of n d-dimensional rectangular ranges, compute the measure of their union. This general problem is Klee's measure problem.
When generalized to the d-dimensional case, Bentley's algorithm has a running time of
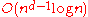. This turns out not to be optimal, because it only decomposes the d-dimensional problem into n (d-1)-dimensional problems, and does not further decompose those subproblems. In 1981, Jan van LeeuwenJan van Leeuwen
Jan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
and Derek Wood improved the running time of this algorithm to
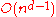for d ≥ 3 by using dynamic quadtreeQuadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes. This...
s.
In 1988, Mark Overmars
Mark Overmars
Markus Hendrik Overmars is a Dutch computer scientist and teacher of game programming known for his game development application Game Maker. Game Maker lets people create computer games using a drag-and-drop interface. He is the head of the Center for Geometry, Imaging, and Virtual Environments...
and Chee Yap proposed an
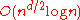algorithm for d ≥ 3 which is the fastest known algorithm to date. Their algorithm uses a particular data structure similar to a kd-treeKd-tree
In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key...
to decompose the problem into 2-dimensional components and aggregate those components efficiently; the 2-dimensional problems themselves are solved efficiently using a trellis
Trellis (graph)
A trellis is a graph of which the nodes are ordered into vertical slices and each node at each time is connected to at least one node at an earlier and at least one node at a later time. The earliest and latest times in the trellis have only one node.Trellises are used in encoders and decoders for...
structure. Although asymptotically faster than Bentley's algorithm, its data structures use significantly more space, so it is only used in problems where either n or d is large. In 1998, Bogdan Chlebus proposed a simpler algorithm with the same asymptotic running time for the common special cases where d is 3 or 4.
Current status
The only known lower bound for any d is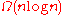. The Overmars–Yap algorithm provides an upper bound of 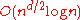, so for d ≥ 3, it remains an open question whether faster algorithms are possible, or alternatively whether tighter lower bounds can be proven. In particular, it remains open whether the algorithm's running time must depend on d. In addition, the question of whether there are faster algorithms that can deal with special cases (for example, when the input coordinates are integers within a bounded range) remains open.Secondary literature
- Franco P. PreparataFranco P. PreparataFranco P. Preparata is a computer scientist, the An Wang Professor of Computer Science at Brown University. He is best known for his 1985 computational geometry book with Michael Shamos, for many years the standard textbook in the field, but Preparata has worked in many other areas of computer...
and Michael I. ShamosMichael Ian ShamosMichael Ian Shamos is an American mathematician, attorney, book author, journal editor, consultant and company director. He is Michael Ian Shamos (born April 21, 1947, and often referred to as Mike Shamos) is an American mathematician, attorney, book author, journal editor, consultant and company...
(1985). Computational Geometry (Springer-Verlag, Berlin). - Klee's Measure Problem, from Professor Jeff Erickson's list of open problems in computational geometry. (Accessed November 8, 2005, when the last update was July 31, 1998.)