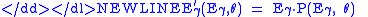The Klein–Nishina formula
gives the differential cross section of photons scattered from a single free electron in lowest order of
quantum electrodynamics

Quantum electrodynamics

Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...

. At low frequencies (e.g., visible light) this is referred to as
Thomson scattering

Thomson scattering

Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is just the low-energy limit of Compton scattering: the particle kinetic energy and photon frequency are the same before and after the scattering...

; at higher frequencies (e.g., x-ray

X-ray

X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...

s and gamma-rays) this is referred
to as Compton scattering

Compton scattering

In physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy of an X-ray or gamma ray photon, called the Compton effect...

.

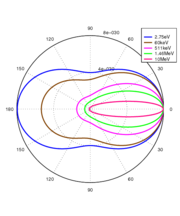
For an incident photon of energy 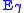, the differential cross section

Cross section (physics)

A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....

 is:

where is the fine structure constant (~1/137.04), 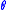is the scattering angle; 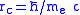is the Compton wave length of the electron (~0.38616 pm); 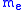is the mass of an electron (~511 keV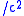); and 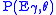is the ratio of photon energy after and before the collision:

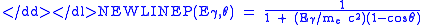
Note that this result may also be expressed in terms of the
classical electron radius

Classical electron radius

The classical electron radius, also known as the Lorentz radius or the Thomson scattering length, is based on a classical relativistic model of the electron...

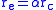 . While this classical quantity is not particularly relevant
in quantum electrodynamics, it is easy to appreciate: in the forward direction (for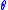 ~ 0), photons scatter off electrons as if these were about 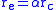(~2.8179 fm) in linear dimension, and 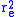(~ 7.9406x10 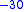m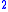 or 79.406 mb) in size

The Klein–Nishina formula was derived in 1928 by Oskar Klein

Oskar Klein

Oskar Benjamin Klein was a Swedish theoretical physicist.Klein was born in Danderyd outside Stockholm, son of the chief rabbi of Stockholm, Dr. Gottlieb Klein from Homonna in Hungary and Antonie Levy...

 and Yoshio Nishina

Yoshio Nishina

was the founding father of modern physics research in Japan. He co-authored the well-known Klein–Nishina formula. He was a principal investigator of RIKEN and mentored generations...

, and was one of the first results obtained from the study of quantum electrodynamics

Quantum electrodynamics

Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...

. Consideration of relativistic and quantum mechanical effects allowed development of an accurate equation for the scattering of radiation from a target electron. Before this derivation, the electron cross section had been classically derived by the British physicist and discoverer of the electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

, J.J. Thomson. However, scattering experiments showed significant deviations from the results predicted by the Thomson cross section. Further scattering experiments agreed perfectly with the predictions of the Klein–Nishina formula.

Note that if ,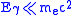
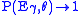and the Klein–Nishina formula reduces to the classical Thomson expression.

The final energy of the scattered photon,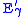 , depends only on the scattering angle and the original photon energy, and so it can be computed without the use of the Klein–Nishina formula:

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.