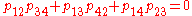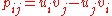Klein quadric
Encyclopedia
The lines of a 3-dimensional projective space
, S, can be viewed as points of a 5-dimensional projective space, T. In that 5-space, the points that represent a line in S lie on a hyperbolic quadric, Q known as the Klein quadric.
If the underlying vector space
of S is the 4-dimensional vector space V, then T has as underlying vector space the 6-dimensional exterior square Λ2V of V. The line coordinates
obtained this way are known as Plücker coordinates
.
These Plücker coordinates satisfy the quadratic relation
defining Q, where
are the coordinates of the line spanned by the two vectors u and v.
The 3-space, S, can be reconstructed again from the quadric, Q: the planes contained in Q fall into two equivalence classes, where planes in the same class meet in a point, and planes in different classes meet in a line or in the empty set. Let these classes be and
and  . The geometry
. The geometry
of S is retrieved as follows:
The fact that the geometries of S and Q are isomorphic can be explained by the isomorphism of the Dynkin diagrams A3 and D3.
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, S, can be viewed as points of a 5-dimensional projective space, T. In that 5-space, the points that represent a line in S lie on a hyperbolic quadric, Q known as the Klein quadric.
If the underlying vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of S is the 4-dimensional vector space V, then T has as underlying vector space the 6-dimensional exterior square Λ2V of V. The line coordinates
Line coordinates
In geometry, line coordinates are used to specify the position of a line just as point coordinates are used to specify the position of a point.-Lines in the plane:...
obtained this way are known as Plücker coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
.
These Plücker coordinates satisfy the quadratic relation
defining Q, where
are the coordinates of the line spanned by the two vectors u and v.
The 3-space, S, can be reconstructed again from the quadric, Q: the planes contained in Q fall into two equivalence classes, where planes in the same class meet in a point, and planes in different classes meet in a line or in the empty set. Let these classes be
 and
and  . The geometry
. The geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
of S is retrieved as follows:
- The points of S are the planes in C.
- The lines of S are the points of Q.
- The planes of S are the planes in C’.
The fact that the geometries of S and Q are isomorphic can be explained by the isomorphism of the Dynkin diagrams A3 and D3.