Kleinian model
Encyclopedia
In mathematics
, a Kleinian model is a model of a three-dimensional hyperbolic manifold
N by the quotient space
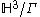where Γ is a discrete subgroup
of PSL(2,C). Here, the subgroup Γ, a Kleinian group
, is defined so that it is isomorphic to the fundamental group
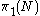of the surface N. Many authors use the terms Kleinian group and Kleinian model interchangeably, letting one stand for the other. See also hyperbolic 3-manifold
.
Many properties of Kleinian models are in direct analogy to those of Fuchsian model
s; however, overall, the theory is less well developed. A number of unsolved conjectures on Kleinian models are the analogs to theorems on Fuchsian models.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kleinian model is a model of a three-dimensional hyperbolic manifold
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
N by the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
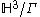where Γ is a discrete subgroupDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
of PSL(2,C). Here, the subgroup Γ, a Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
, is defined so that it is isomorphic to the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
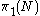of the surface N. Many authors use the terms Kleinian group and Kleinian model interchangeably, letting one stand for the other. See also hyperbolic 3-manifoldHyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
.
Many properties of Kleinian models are in direct analogy to those of Fuchsian model
Fuchsian model
In mathematics, a Fuchsian model is a construction of a hyperbolic Riemann surface R as a quotient of the upper half-plane H. By the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Every hyperbolic Riemann surface has a non-trivial fundamental group \pi_1...
s; however, overall, the theory is less well developed. A number of unsolved conjectures on Kleinian models are the analogs to theorems on Fuchsian models.