
Knaster-Kuratowski fan
Encyclopedia
In topology
, a branch of mathematics, the Knaster–Kuratowski fan (also known as Cantor's leaky tent or Cantor's teepee depending on the presence or absence of the apex
) is a connected
topological space
with the property that the removal of a single point makes it totally disconnected.
Let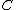 be the Cantor set
be the Cantor set
, let be the point
be the point 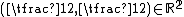 , and let
, and let 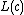 , for
, for  , denote the line segment connecting
, denote the line segment connecting  to
to 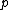 . If
. If  is an endpoint of an interval deleted in the Cantor set, let
is an endpoint of an interval deleted in the Cantor set, let 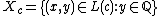 ; for all other points in
; for all other points in 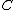 let
let 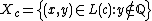 ; the Knaster–Kuratowski fan is defined as
; the Knaster–Kuratowski fan is defined as 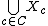 .
.
The fan itself is connected, but becomes totally disconnected upon the removal of .
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a branch of mathematics, the Knaster–Kuratowski fan (also known as Cantor's leaky tent or Cantor's teepee depending on the presence or absence of the apex
Apex (geometry)
In geometry, an apex is the vertex which is in some sense the highest of the figure to which it belongs.*In an isosceles triangle, the apex is the vertex where the two sides of equal length meet, opposite the unequal third side....
) is a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with the property that the removal of a single point makes it totally disconnected.
Let
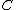 be the Cantor set
be the Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, let
 be the point
be the point 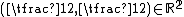 , and let
, and let 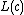 , for
, for  , denote the line segment connecting
, denote the line segment connecting  to
to 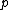 . If
. If  is an endpoint of an interval deleted in the Cantor set, let
is an endpoint of an interval deleted in the Cantor set, let 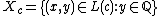 ; for all other points in
; for all other points in 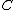 let
let 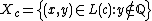 ; the Knaster–Kuratowski fan is defined as
; the Knaster–Kuratowski fan is defined as 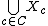 .
.The fan itself is connected, but becomes totally disconnected upon the removal of
 .
.

