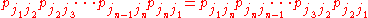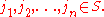Kolmogorov’s criterion
Encyclopedia
In probability theory
, Kolmogorov's criterion, named after Andrey Kolmogorov
, is a theorem
in Markov process
es concerning stationary Markov chain
s (i.e. ones with stationary transition probabilities, also called "time-homogeneous Markov chains"). The theorem states that such a chain is reversible
if and only if its transition probabilities satisfy
for all finite sequences of states
Here pij are elements of the transition matrix P and S is the state space of the chain.
Proofs of this theorem are available in the literature.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Kolmogorov's criterion, named after Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es concerning stationary Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s (i.e. ones with stationary transition probabilities, also called "time-homogeneous Markov chains"). The theorem states that such a chain is reversible
Time reversibility
Time reversibility is an attribute of some stochastic processes and some deterministic processes.If a stochastic process is time reversible, then it is not possible to determine, given the states at a number of points in time after running the stochastic process, which state came first and which...
if and only if its transition probabilities satisfy
for all finite sequences of states
Here pij are elements of the transition matrix P and S is the state space of the chain.
Proofs of this theorem are available in the literature.