
Korn's inequality
Encyclopedia
In mathematics
, Korn's inequality is a result about the derivative
s of Sobolev functions
. Korn's inequality plays an important role in linear elasticity theory.
, connected
domain in n-dimension
al Euclidean space
Rn, n ≥ 2. Let H1(Ω) be the Sobolev space of all vector field
s v = (v1, ..., vn) on Ω that, along with their weak derivatives, lie in the Lebesgue space
L2(Ω). Denoting the partial derivative
with respect to the ith component by ∂i, the norm
in H1(Ω) is given by
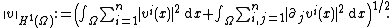
Then there is a constant C ≥ 0, known as the Korn constant of Ω, such that, for all v ∈ H1(Ω),
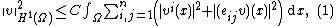
where e denotes the symmetrized gradient given by
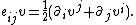
Inequality (1) is known as Korn's inequality.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Korn's inequality is a result about the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of Sobolev functions
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
. Korn's inequality plays an important role in linear elasticity theory.
Statement of the inequality
Let Ω be an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
domain in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, n ≥ 2. Let H1(Ω) be the Sobolev space of all vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s v = (v1, ..., vn) on Ω that, along with their weak derivatives, lie in the Lebesgue space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
L2(Ω). Denoting the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to the ith component by ∂i, the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
in H1(Ω) is given by
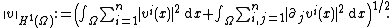
Then there is a constant C ≥ 0, known as the Korn constant of Ω, such that, for all v ∈ H1(Ω),
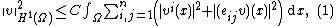
where e denotes the symmetrized gradient given by
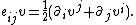
Inequality (1) is known as Korn's inequality.

