
Kronecker limit formula
Encyclopedia
In mathematics, the classical Kronecker limit formula describes the constant term at s = 1 of a real analytic Eisenstein series
(or Epstein zeta function) in terms of the Dedekind eta function
. There are many generalizations of it to more complicated Eisenstein series. It is named for Leopold Kronecker
.
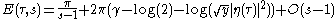
where
for Re(s) > 1, and by analytic continuation for other values of the complex number s.
So the Eisenstein series has a pole at s = 1 of residue π, and the (first) Kronecker limit formula gives the constant term of the Laurent series
at this pole.
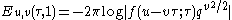
where
for Re(s) > 1, and is defined by analytic continuation for other values of the complex number s.
Real analytic Eisenstein series
In mathematics, the simplest real analytic Eisenstein series is a special function of two variables. It is used in the representation theory of SL and in analytic number theory...
(or Epstein zeta function) in terms of the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. There are many generalizations of it to more complicated Eisenstein series. It is named for Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
.
First Kronecker limit formula
The (first) Kronecker limit formula states that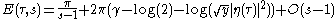
where
- E(τ,s) is the real analytic Eisenstein series, given by

for Re(s) > 1, and by analytic continuation for other values of the complex number s.
- γ is Euler-Mascheroni constantEuler-Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
- τ = x + iy with y > 0.
-
 , with q = e2π i τ is the Dedekind eta functionDedekind eta functionThe Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
, with q = e2π i τ is the Dedekind eta functionDedekind eta functionThe Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
.
So the Eisenstein series has a pole at s = 1 of residue π, and the (first) Kronecker limit formula gives the constant term of the Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
at this pole.
Second Kronecker limit formula
The second Kronecker limit formula states that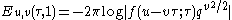
where
- u and v are real and not both integers.
- q = e2π i τ and qa = e2π i aτ
- p = e2π i z and pa = e2π i az
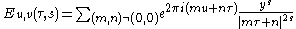
for Re(s) > 1, and is defined by analytic continuation for other values of the complex number s.


