In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, the Kruskal–Wallis one-way analysis of variance by ranks (named after William Kruskal

William Kruskal

William Henry Kruskal was an American mathematician and statistician. He is best known for having formulated the Kruskal–Wallis one-way analysis of variance , a widely-used nonparametric statistical method.Kruskal was born in New York City to a successful fur wholesaler...

 and W. Allen Wallis) is a non-parametric method

Non-parametric statistics

In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...

 for testing whether samples originate from the same distribution. The factual null hypothesis is that the populations from which the samples originate, have the same median

Median

In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...

. It is identical to a one-way analysis of variance

Analysis of variance

In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...

 with the data replaced by their ranks. It is an extension of the Mann–Whitney U test to 3 or more groups.

Since it is a non-parametric method, the Kruskal–Wallis test does not assume a normal population, unlike the analogous one-way analysis of variance

Analysis of variance

In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...

. However, the test does assume an identically-shaped and scaled distribution for each group, except for any difference in median

Median

In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...

s.

Method

1. Rank all data from all groups together; i.e., rank the data from 1 to N ignoring group membership. Assign any tied values the average of the ranks they would have received had they not been tied.
2. The test statistic is given by:

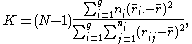   where:

   • is the number of observations in group
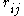   • is the rank (among all observations) of observation from group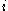
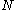   • is the total number of observations across all groups
   • ,
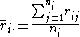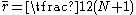   • is the average of all the .
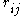3. Notice that the denominator of the expression for 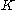is exactly 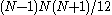and 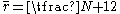. Thus

   
   Notice that the last formula only contains the squares of the average ranks.

   1. A correction for ties can be made by dividing by 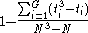, where G is the number of groupings of different tied ranks, and t_i is the number of tied values within group i that are tied at a particular value. This correction usually makes little difference in the value of K unless there are a large number of ties.
   2. Finally, the p-value
      P-value
      In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
      
       is approximated by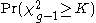 . If some 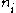values are small (i.e., less than 5) the probability distribution
      Probability distribution
      In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
      
       of K can be quite different from this chi-squared distribution. If a table of the chi-squared probability distribution is available, the critical value of chi-squared,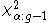 , can be found by entering the table at g − 1 degrees of freedom
      Degrees of freedom (statistics)
      In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
      
       and looking under the desired significance
      Statistical significance
      In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
      
       or alpha level. The null hypothesis
      Null hypothesis
      The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
      
       of equal population median
      Median
      In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
      
      s would then be rejected if . Appropriate multiple comparisons
      Multiple comparisons
      In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
      
      would then be performed on the group medians.

   The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.