Kuhn length
Encyclopedia
The Kuhn length is a theoretical treatment, developed by Werner Kuhn
, in which a real polymer
chain is considered as a collection of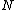
Kuhn segments each with a Kuhn length 
. Each Kuhn segment can be thought of as if they are freely jointed with each other. Each segment in a freely jointed chain can randomly orient in any direction without the influence of any forces, independent of the directions taken by other segments. Thus the real chain consisting of 
bonds and with fixed bond angles and bond lengths is replaced by an equivalent chain with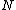 
connected Kuhn segments that can orient in any random direction. The length of a fully stretched chain or the contour length is 
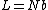for the Kuhn segment chain. In the simplest treatment, such a chain follows the random walk model, where each step taken in a random direction is independent of the directions taken in the previous steps, forming a random coil
. The average end-to-end distance for a chain satisfying the random walk model is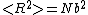
. Since the space occupied by a segment in the polymer chain cannot be taken by another segment, a self-avoiding random walk model can also be used. The Kuhn segment construction is useful in that it allows complicated polymers to be treated with simplified models as either a random walk
or a self-avoiding walk
, which can simplify the treatment considerably.
For an actual homopolymer chain (consists of the same repeat units) with bond length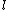
and bond angle θ with a dihedral angle
energy potential, the average end-to-end distance can be obtained as
, where 
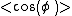is the average cosine of the dihedral angle. Also the fully stretched length 
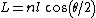. By equating 
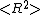and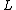 
for the actual chain and the equivalent chain with Kuhn segments, the number of Kuhn segments 
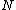and the Kuhn segment length 
can be obtained.
For semiflexible chain
, Kuhn length equals two times the persistence length
.
Werner Kuhn
Werner Kuhn is a Swiss physical chemist who developed the first model of the viscosity of polymer solutions using statistical mechanics. He is known for being the first to apply Boltzmann's entropy formula:S = k \log W \!...
, in which a real polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
chain is considered as a collection of
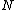Kuhn segments each with a Kuhn length . Each Kuhn segment can be thought of as if they are freely jointed with each other. Each segment in a freely jointed chain can randomly orient in any direction without the influence of any forces, independent of the directions taken by other segments. Thus the real chain consisting of bonds and with fixed bond angles and bond lengths is replaced by an equivalent chain with 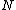connected Kuhn segments that can orient in any random direction. The length of a fully stretched chain or the contour length is 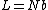for the Kuhn segment chain. In the simplest treatment, such a chain follows the random walk model, where each step taken in a random direction is independent of the directions taken in the previous steps, forming a random coilRandom coil
A random coil is a polymer conformation where the monomer subunits are oriented randomly while still being bonded to adjacent units. It is not one specific shape, but a statistical distribution of shapes for all the chains in a population of macromolecules...
. The average end-to-end distance for a chain satisfying the random walk model is
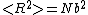. Since the space occupied by a segment in the polymer chain cannot be taken by another segment, a self-avoiding random walk model can also be used. The Kuhn segment construction is useful in that it allows complicated polymers to be treated with simplified models as either a random walkRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
or a self-avoiding walk
Self-avoiding walk
In mathematics, a self-avoiding walk is a sequence of moves on a lattice that does not visit the same point more than once. A self-avoiding polygon is a closed self-avoiding walk on a lattice...
, which can simplify the treatment considerably.
For an actual homopolymer chain (consists of the same repeat units) with bond length
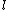and bond angle θ with a dihedral angleDihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
energy potential, the average end-to-end distance can be obtained as
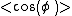, where is the average cosine of the dihedral angle. Also the fully stretched length 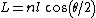. By equating 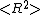and 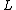for the actual chain and the equivalent chain with Kuhn segments, the number of Kuhn segments 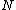and the Kuhn segment length can be obtained.For semiflexible chain
Worm-like chain
The worm-like chain model in polymer physics is used to describe the behavior of semi-flexible polymers; it is sometimes referred to as the Kratky-Porod model.- Theoretical Considerations :...
, Kuhn length equals two times the persistence length
Persistence length
The persistence length is a basic mechanical property quantifying the stiffness of a polymer or of a string.Informally, for pieces of the polymer that are shorter than the persistence length, the molecule behaves rather like a flexible elastic rod, while for pieces of the polymer that are much...
.