Kuramoto model
Encyclopedia
The Kuramoto model, first proposed by Yoshiki Kuramoto
(蔵本 由紀 Kuramoto Yoshiki), is a mathematical model
used to describe synchronization
. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological
oscillators, and it has found widespread applications such as in neuroscience.
The model makes several assumptions, including that there is weak coupling, that the oscillators are identical or nearly identical, and that interactions depend sinusoidally on the phase difference between each pair of objects.
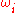, and each is coupled equally to all other oscillators. Surprisingly, this fully nonlinear model can be solved exactly, in the infinite-N limit, with a clever transformation and the application of self-consistency arguments.
The most popular form of the model has the following governing equations:
,
where the system is composed of N limit-cycle oscillators.
Noise can be added to the system. In that case, the original equation is altered to: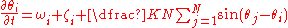
,
where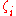
is the fluctuation and a function of time. If we consider the noise to be white noise, then
,
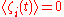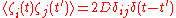
with
denoting the strength of noise.
Define the "order" parameters r and ψ as
.
Here r represents the phase-coherence
of the population of oscillators, and ψ indicates the average phase. Applying this transformation, the governing equation becomes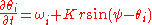
.
Thus the oscillators' equations are no longer explicitly coupled; instead the order parameters govern behavior. A further transformation is usually done, to a rotating frame in which the statistical average of phases over all oscillators is zero. That is,
. Finally, the governing equation becomes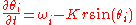
.
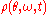. Normalization requires that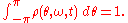
The continuity equation
for oscillator density will be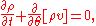
where v is the drift velocity of the oscillators given by taking the infinite-N limit in the transformed governing equation, i.e.,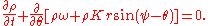
Finally, we must rewrite the definition of the order parameters for the continuum (infinite N) limit.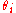
must be replaced by its ensemble average (over all ω) and the sum must be replaced by an integral, to give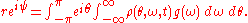
state with all oscillators drifting randomly corresponds to the solution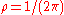
. In that case 
, and there is no coherence among the oscillators. They are uniformly distributed across all possible phases, and the population is in a statistical steady-state (although individual oscillators continue to change phase in accordance with their intrinsic ω).
When coupling K is sufficiently strong, a fully synchronized solution is possible. In the fully synchronized state, all the oscillators share a common frequency, although their phases are different.
A solution for the case of partial synchronization yields a state in which only some oscillators (those near the ensemble's mean natural frequency) synchronize; other oscillators drift incoherently. Mathematically, the state has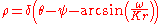
for locked oscillators, and
for drifting oscillators. The cutoff occurs when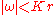
.
Yoshiki Kuramoto
is a Japanese physicist in the Nonlinear Dynamics group at Kyoto University who formulated the Kuramoto model.-Notes:...
(蔵本 由紀 Kuramoto Yoshiki), is a mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
used to describe synchronization
Synchronization
Synchronization is timekeeping which requires the coordination of events to operate a system in unison. The familiar conductor of an orchestra serves to keep the orchestra in time....
. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological
Biological process
A biological process is a process of a living organism. Biological processes are made up of any number of chemical reactions or other events that results in a transformation....
oscillators, and it has found widespread applications such as in neuroscience.
The model makes several assumptions, including that there is weak coupling, that the oscillators are identical or nearly identical, and that interactions depend sinusoidally on the phase difference between each pair of objects.
Definition
In the most popular version of the Kuramoto model, each of the oscillators is considered to have its own intrinsic natural frequency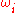, and each is coupled equally to all other oscillators. Surprisingly, this fully nonlinear model can be solved exactly, in the infinite-N limit, with a clever transformation and the application of self-consistency arguments.The most popular form of the model has the following governing equations:
,where the system is composed of N limit-cycle oscillators.
Noise can be added to the system. In that case, the original equation is altered to:
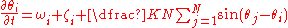,where
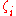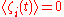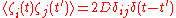
is the fluctuation and a function of time. If we consider the noise to be white noise, then ,with
denoting the strength of noise.Transformation
The transformation that allows this model to be solved exactly (at least in the N → ∞ limit) is as follows.Define the "order" parameters r and ψ as
.Here r represents the phase-coherence
Coherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
of the population of oscillators, and ψ indicates the average phase. Applying this transformation, the governing equation becomes
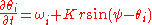.Thus the oscillators' equations are no longer explicitly coupled; instead the order parameters govern behavior. A further transformation is usually done, to a rotating frame in which the statistical average of phases over all oscillators is zero. That is,
. Finally, the governing equation becomes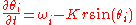.Large N limit
Now consider the case as N tends to infinity. Take the distribution of intrinsic natural frequencies as g(ω) (assumed normalized). Then assume that the density of oscillators at a given phase θ, with given natural frequency ω, at time t is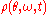. Normalization requires that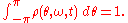The continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
for oscillator density will be
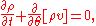
where v is the drift velocity of the oscillators given by taking the infinite-N limit in the transformed governing equation, i.e.,
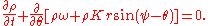
Finally, we must rewrite the definition of the order parameters for the continuum (infinite N) limit.
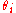must be replaced by its ensemble average (over all ω) and the sum must be replaced by an integral, to give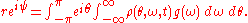Solutions
The incoherentCoherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
state with all oscillators drifting randomly corresponds to the solution
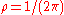. In that case , and there is no coherence among the oscillators. They are uniformly distributed across all possible phases, and the population is in a statistical steady-state (although individual oscillators continue to change phase in accordance with their intrinsic ω).When coupling K is sufficiently strong, a fully synchronized solution is possible. In the fully synchronized state, all the oscillators share a common frequency, although their phases are different.
A solution for the case of partial synchronization yields a state in which only some oscillators (those near the ensemble's mean natural frequency) synchronize; other oscillators drift incoherently. Mathematically, the state has
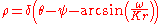
for locked oscillators, and
for drifting oscillators. The cutoff occurs when
.
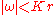