Kuratowski's closure-complement problem
Encyclopedia
In point-set topology, Kuratowski's closure-complement problem asks for the largest number of distinct sets obtainable by repeatedly applying the set operations of closure
and complement
to a given starting subset of a topological space
. The answer is 14. This result was first published by Kazimierz Kuratowski
in 1922. The problem gained wide exposure three decades later as an exercise in John L. Kelley
's classic textbook General Topology.
of S, and cS for the complement of S. The following three identities imply that no more than 14 distinct sets are obtainable:
(1) kkS = kS
(2) ccS = S
(3) kckckckS = kckS.
The first two are trivial. The third follows from the identities kikiS = kiS and iS = ckcS.
A subset realizing the maximum of 14 is called a 14-set. The space of real numbers under the usual topology contains 14-sets. Here is one example: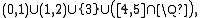
where
denotes an open interval and 
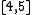denotes a closed interval.
ic than topological. A surprising abundance of closely related problems and results have appeared since 1960, many of which have little or nothing to do with point-set topology.
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
and complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
to a given starting subset of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. The answer is 14. This result was first published by Kazimierz Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
in 1922. The problem gained wide exposure three decades later as an exercise in John L. Kelley
John L. Kelley
John Leroy Kelley was an American mathematician at University of California, Berkeley who worked in general topology and functional analysis....
's classic textbook General Topology.
Proof
Letting S denote an arbitrary subset of a topological space, write kS for the closure of S, iS for the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of S, and cS for the complement of S. The following three identities imply that no more than 14 distinct sets are obtainable:
(1) kkS = kS
(2) ccS = S
(3) kckckckS = kckS.
The first two are trivial. The third follows from the identities kikiS = kiS and iS = ckcS.
A subset realizing the maximum of 14 is called a 14-set. The space of real numbers under the usual topology contains 14-sets. Here is one example:
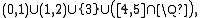
where
denotes an open interval and 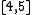denotes a closed interval.Further results
Despite its origin within the context of a topological space, Kuratowski's closure-complement problem is actually more algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic than topological. A surprising abundance of closely related problems and results have appeared since 1960, many of which have little or nothing to do with point-set topology.
External links
- The Kuratowski Closure-Complement Theorem by B. J. Gardner and Marcel Jackson