
König's theorem (set theory)
Encyclopedia
In set theory
, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the name Julius König
) colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal number
s for every i in I, and for every i in I then
for every i in I then
The sum here is the cardinality of the disjoint union
of the sets mi and the product is the cardinality of the cartesian product
. However, this formulation cannot even be stated without the use of some form of the Axiom of Choice.
 for every i in I then
for every i in I then
where < means strictly less than in cardinality, i.e. there is an injective function
from Ai to Bi, but not one going the other way. The union involved need not be disjoint (a non-disjoint union can't be any bigger than the disjoint version, also assuming the axiom of choice). In this formulation, König's theorem is equivalent to the Axiom of Choice.
(Of course, König's theorem is trivial if the cardinal numbers mi and ni are finite and the index set I is finite. If I is empty
, then the left sum is the empty sum and therefore 0, while the right hand product is the empty product
and therefore 1).
König's theorem is remarkable because of the strict inequality in the conclusion. There are many easy rules for the arithmetic of infinite sums and products of cardinals in which one can only conclude a weak inequality ≤, for example: IF for all i in I, THEN one can only conclude
for all i in I, THEN one can only conclude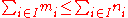
since, for example, setting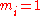 &
&  where the index set I is the natural numbers, yields the sum
where the index set I is the natural numbers, yields the sum 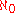 for both sides and we have a strict equality.
for both sides and we have a strict equality.
If we take mi = 1, and ni = 2 for each i in κ, then the left hand side of the above inequality is just κ, while the right hand side is 2κ, the cardinality of functions from κ to {0,1}, that is, the cardinality of the power set of κ. Thus, König's theorem gives us an alternate proof of Cantor's theorem
. (Historically of course Cantor's theorem was proved much earlier.)
That is, the Cartesian product of the given non-empty sets, Bi, has a larger cardinality than the sum of empty sets. Thus it is non-empty which is just what the axiom of choice states. Since the axiom of choice follows from König's theorem, we will use the axiom of choice freely and implicitly when discussing consequences of the theorem.
of cardinal numbers.
Choose a strictly increasing cf(κ)-sequence of cardinals approaching κ. Each of them is less than κ, so their sum which is κ is less than the product of cf(κ) copies of κ.
According to Easton's theorem
, the next consequence of König's theorem is the only nontrivial constraint on the continuum function for regular cardinal
s.
Let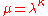 . Suppose that, contrary to this corollary,
. Suppose that, contrary to this corollary, 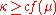 . Then using the previous corollary,
. Then using the previous corollary, 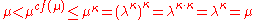 , a contradiction. Thus the supposition must be false and this corollary must be true.
, a contradiction. Thus the supposition must be false and this corollary must be true.
, including especially the axiom of choice, we can prove the theorem. Remember that we are given , and we want to show :
, and we want to show :
First, we show that there is an injection
from the sum to the product. Using the axiom of choice, for each i we choose an injection fi from Ai to Bi. Notice that fi cannot be a surjection because then its inverse would be an injection from Bi to Ai. So, for each i, there must be an element of Bi not in the range of fi. Using the axiom of choice again, we choose such an xi for each i. Define g on the sum by g(i,a) (j) = fi(a) when j = i and a is an element of Ai and g(i,a) (j) = xj when j ≠ i and a is an element of Ai. Since fi(a) ≠ xi for each i, g is an injection from the sum to the product.
Second, we show that there is no injection h from the product to the sum. Suppose, to the contrary, that such an h existed. In a similar manner to Cantor's diagonal argument
, we will construct an element e of the product, which cannot have a value under h. For each i in I, construct a partial function fi from Ai to Bi by fi(a) = d(i) if there is a d in the product such that h(d) = (i,a). (This is a partial function because h is an injection, so the d is unique.) If fi were a surjection, then, using the axiom of choice, we could construct an injection g from Bi into Ai (g would be a right inverse of fi), contradicting the hypothesis. Hence, for each i in I, there are elements of Bi not in the image of fi. So using the axiom of choice again, we choose e(i) in Bi but not in the image of fi. Consider, now, the value of h(e) = (i,c) with c in Ai. But then fi(c) = e(i), contradicting the construction of e. Hence no such injection can exist, and the product is strictly larger in cardinality than the sum.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the name Julius König
Julius König
Gyula Kőnig was a Hungarian mathematician. He was born in Győr, Hungary and died in Budapest. His mathematical publications in foreign languages appeared under the name Julius König...
) colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s for every i in I, and
 for every i in I then
for every i in I then
The sum here is the cardinality of the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of the sets mi and the product is the cardinality of the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
. However, this formulation cannot even be stated without the use of some form of the Axiom of Choice.
Details
The precise statement of the result: if I is a set , Ai and Bi are sets for every i in I, and for every i in I then
for every i in I then
where < means strictly less than in cardinality, i.e. there is an injective function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from Ai to Bi, but not one going the other way. The union involved need not be disjoint (a non-disjoint union can't be any bigger than the disjoint version, also assuming the axiom of choice). In this formulation, König's theorem is equivalent to the Axiom of Choice.
(Of course, König's theorem is trivial if the cardinal numbers mi and ni are finite and the index set I is finite. If I is empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, then the left sum is the empty sum and therefore 0, while the right hand product is the empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
and therefore 1).
König's theorem is remarkable because of the strict inequality in the conclusion. There are many easy rules for the arithmetic of infinite sums and products of cardinals in which one can only conclude a weak inequality ≤, for example: IF
 for all i in I, THEN one can only conclude
for all i in I, THEN one can only conclude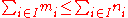
since, for example, setting
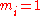 &
&  where the index set I is the natural numbers, yields the sum
where the index set I is the natural numbers, yields the sum 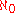 for both sides and we have a strict equality.
for both sides and we have a strict equality.Corollaries of König's theorem
- If
 is a cardinal then
is a cardinal then 
If we take mi = 1, and ni = 2 for each i in κ, then the left hand side of the above inequality is just κ, while the right hand side is 2κ, the cardinality of functions from κ to {0,1}, that is, the cardinality of the power set of κ. Thus, König's theorem gives us an alternate proof of Cantor's theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
. (Historically of course Cantor's theorem was proved much earlier.)
Axiom of choice
One way of stating the axiom of choice is "An arbitrary Cartesian product of non-empty sets is non-empty.". Let Bi be a non-empty set for each i in I. Let Ai = {} for each i in I. Thus by König's theorem, we have:- If
 , then
, then 
That is, the Cartesian product of the given non-empty sets, Bi, has a larger cardinality than the sum of empty sets. Thus it is non-empty which is just what the axiom of choice states. Since the axiom of choice follows from König's theorem, we will use the axiom of choice freely and implicitly when discussing consequences of the theorem.
König's theorem and cofinality
König's theorem has also important consequences for cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
of cardinal numbers.
- If
 , then
, then 
Choose a strictly increasing cf(κ)-sequence of cardinals approaching κ. Each of them is less than κ, so their sum which is κ is less than the product of cf(κ) copies of κ.
According to Easton's theorem
Easton's theorem
In set theory, Easton's theorem is a result on the possible cardinal numbers of powersets. showed via forcing that...
, the next consequence of König's theorem is the only nontrivial constraint on the continuum function for regular cardinal
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
s.
- If
 and
and  , then
, then 
Let
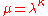 . Suppose that, contrary to this corollary,
. Suppose that, contrary to this corollary, 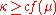 . Then using the previous corollary,
. Then using the previous corollary, 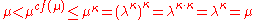 , a contradiction. Thus the supposition must be false and this corollary must be true.
, a contradiction. Thus the supposition must be false and this corollary must be true.A proof of König's theorem
Assuming Zermelo–Fraenkel set theoryZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, including especially the axiom of choice, we can prove the theorem. Remember that we are given
 , and we want to show :
, and we want to show :
First, we show that there is an injection
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from the sum to the product. Using the axiom of choice, for each i we choose an injection fi from Ai to Bi. Notice that fi cannot be a surjection because then its inverse would be an injection from Bi to Ai. So, for each i, there must be an element of Bi not in the range of fi. Using the axiom of choice again, we choose such an xi for each i. Define g on the sum by g(i,a) (j) = fi(a) when j = i and a is an element of Ai and g(i,a) (j) = xj when j ≠ i and a is an element of Ai. Since fi(a) ≠ xi for each i, g is an injection from the sum to the product.
Second, we show that there is no injection h from the product to the sum. Suppose, to the contrary, that such an h existed. In a similar manner to Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
, we will construct an element e of the product, which cannot have a value under h. For each i in I, construct a partial function fi from Ai to Bi by fi(a) = d(i) if there is a d in the product such that h(d) = (i,a). (This is a partial function because h is an injection, so the d is unique.) If fi were a surjection, then, using the axiom of choice, we could construct an injection g from Bi into Ai (g would be a right inverse of fi), contradicting the hypothesis. Hence, for each i in I, there are elements of Bi not in the image of fi. So using the axiom of choice again, we choose e(i) in Bi but not in the image of fi. Consider, now, the value of h(e) = (i,c) with c in Ai. But then fi(c) = e(i), contradicting the construction of e. Hence no such injection can exist, and the product is strictly larger in cardinality than the sum.
External links
- König's theorem article on PlanetMath, includes a proof

