
L-balance theorem
Encyclopedia
In mathematical finite group theory, the L-balance theorem was proved by .
The letter L stands for the layer of a group, and "balance" refers to the property discussed below.
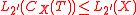
Here L2′(X) stands for the 2-layer of a group X, which is the product of all the 2-components of the group, the minimal subnormal subgroups of X mapping onto components of X/O(X).
A consequence is that if a and b are commuting involutions of a group G then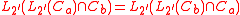
This is the property called L-balance.
More generally similar results are true if the prime 2 is replaced by an prime p, and in this case the condition is called Lp-balance, but the proof of this requires the classification of finite simple groups (more precisely the Schreier conjecture
).
The letter L stands for the layer of a group, and "balance" refers to the property discussed below.
Statement
The L-balance theorem of Gorenstein and Walter states that if X is a finite group and T a 2-subgroup of X then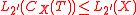
Here L2′(X) stands for the 2-layer of a group X, which is the product of all the 2-components of the group, the minimal subnormal subgroups of X mapping onto components of X/O(X).
A consequence is that if a and b are commuting involutions of a group G then
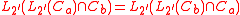
This is the property called L-balance.
More generally similar results are true if the prime 2 is replaced by an prime p, and in this case the condition is called Lp-balance, but the proof of this requires the classification of finite simple groups (more precisely the Schreier conjecture
Schreier conjecture
In finite group theory, the Schreier conjecture asserts that the group of outer automorphisms of every finite simple group is solvable. It was proposed by Otto Schreier in 1926, and is now known to be true as a result of the classification of finite simple groups, but no simpler proof is known....
).

