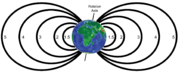
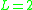The L-shell, L-value, or McIlwain L-parameter (after Carl McIlwain) is a parameter describing a particular set of planetary magnetic field lines. Colloquially, L-value often describes the set of magnetic field lines which cross the Earth's magnetic equator at a number of Earth-radii equal to the L-value. For example, "" describes the set of the Earth's magnetic field

Earth's magnetic field

Earth's magnetic field is the magnetic field that extends from the Earth's inner core to where it meets the solar wind, a stream of energetic particles emanating from the Sun...

 lines which cross the Earth's magnetic equator two earth radii from the center of the Earth. L-shell parameters can also describe the magnetic fields of other planets. In such cases, the parameter is renormalized for that planet's radius and magnetic field model.

Although L-value is formally defined in terms of the Earth's true instantaneous magnetic field (or a high-order model like IGRF), it is often used to give a general picture of magnetic phenomena near the Earth, in which case it can be approximated using the dipole model of the Earth's magnetic field

Dipole model of the Earth's magnetic field

The dipole model of the Earth's magnetic field is a first order approximation of the rather complex true Earth's magnetic field. Due to effects of the interplanetary magnetic field, and the solar wind, the dipole model is particularly inaccurate at high L-shells , but may be a good approximation...

.

Charged particle motions in a dipole field

The motions of low-energy charged particles in the Earth's magnetic field (or in any nearly-dipolar magnetic field) can be usefully described in terms of McIllwain's (B,L)  coordinates, the first of which, B  is just the magnitude (or length) of the magnetic field vector.
This description is most valuable when the gyroradius of the charged particle orbit is small compared to the spatial scale for changes in the field. Then a charged particle will basically follow a helical path orbiting the local field line. In a local coordinate system {x,y,z}  where z  is along the field, the transverse motion will be nearly a circle, orbiting the "guiding center

Guiding center

In many cases of practical interest, the motion in a magnetic field of an electrically charged particle can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point...

", that is the center of the orbit or the local B  line, with the gyroradius and frequency characteristic of cyclotron motion for the field strength, while the simultaneous motion along z  will be at nearly uniform velocity, since the component of the Lorentz force

Lorentz force

In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...

 along the field line is zero.

At the next level of approximation, as the particle orbits and moves along the field line, along which the field changes slowly, the radius of the orbit changes so as to keep the magnetic flux

Magnetic flux

Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...

 enclosed by the orbit constant. Since the Lorentz force is strictly perpendicular to the velocity, it cannot change the energy of a charged particle moving in it. Thus the particle's kinetic energy remains constant. Then so also must its speed be constant. Then it can be shown that the particle's velocity parallel to the local field must decrease if the field is increasing along its z  motion, and increase if the field decreases, while the components of the velocity transverse to the field increase or decrease so as to keep the magnitude of the total velocity constant. Conservation of energy prevents the transverse velocity from increasing without limit, and eventually the longitudinal component of the velocity becomes zero, while the pitch angle

Pitch angle

The pitch angle of a charged particle is the angle between the particle's velocity vector and the local magnetic field. This is a common measurement and topic when studying the magnetosphere. See Aurora and Ring current-Usage: Particle motion:...

, of the particle with respect to the field line, becomes 90°. Then the longitudinal motion is stopped and reversed, and the particle is reflected back towards regions of weaker field, the guiding center now retracing its previous motion along the field line, with the particle's transverse velocity decreasing and its longitudinal velocity increasing.

In the (approximately) dipole field of the Earth, the magnitude of the field is greatest near the magnetic poles, and least near the magnetic Equator. Thus after the particle crosses the Equator, it will again encounter regions of increasing field, until it once again stops at the magnetic mirror point, on the opposite side of the Equator. The result is that, as the particle orbits its guiding center

Guiding center

In many cases of practical interest, the motion in a magnetic field of an electrically charged particle can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point...

 on the field line, it bounces back and forth between the north mirror point and the south mirror point, remaining approximately on the same field line. The particle is therefore endlessly trapped, and cannot escape from the region of the Earth. Particles with too-small pitch angles may strike the top of the atmosphere if they are not mirrored before their field line reaches too close to the Earth, in which case they will eventually be scattered by atoms in the air, lose energy, and be lost from the belts.

However, for particles which mirror at safe altitudes, (in yet a further level of approximation) the fact that the field generally increases towards the center of the Earth means that the curvature on the side of the orbit nearest the Earth is somewhat greater than on the opposite side, so that the orbit has a slightly non-circular, with a (prolate) cycloid

Cycloid

A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....

al shape, and the guiding center slowly moves perpendicular both to the field line and to the radial direction. The guiding center of the cyclotron orbit, instead of moving exactly along the field line, therefore drifts slowly east or west (depending on the sign of the charge of the particle), and the local field line connecting the two mirror points at any moment, slowly sweeps out a surface connecting them as it moves in longitude. Eventually the particle will drift entirely around the Earth, and the surface will be closed upon itself. These drift surfaces, nested like the skin of an onion, are the surfaces of constant L  in the McIlwain coordinate system. They apply not only for a perfect dipole field, but also for fields that are approximately dipolar. For a given particle, as long as only the Lorentz force is involved, B  and L  remain constant and particles can be trapped indefinitely. Use of (B,L)  coordinates provides us with a way of mapping the real, non-dipolar terrestrial or planetary field into coordinates that behave essentially like those of a perfect dipole. The L  parameter is traditionally labeled in Earth-radii, of the point where the shell crosses the magnetic Equator, of the equivalent dipole. B  is measured in gauss.

Equation for L in a Dipole Magnetic Field

In a centered dipole magnetic field model, the path along a given L shell can be described as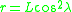



where is the radial distance (in earth radii) to a point on the line, 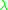is its geomagnetic latitude

Geomagnetic latitude

Geomagnetic latitude is a parameter analogous to geographic latitude, except that bearing is with respect to the magnetic poles, as opposed to the geographic poles....

, and is the L-shell of interest.

L-shells on Earth

For the Earth, L-shells uniquely define regions of particular geophysical interest. Certain physical phenomena occur in the ionosphere

Ionosphere

The ionosphere is a part of the upper atmosphere, comprising portions of the mesosphere, thermosphere and exosphere, distinguished because it is ionized by solar radiation. It plays an important part in atmospheric electricity and forms the inner edge of the magnetosphere...

 and magnetosphere

Magnetosphere

A magnetosphere is formed when a stream of charged particles, such as the solar wind, interacts with and is deflected by the intrinsic magnetic field of a planet or similar body. Earth is surrounded by a magnetosphere, as are the other planets with intrinsic magnetic fields: Mercury, Jupiter,...

 at characteristic L-shells. For instance, auroral light displays

Aurora (astronomy)

An aurora is a natural light display in the sky particularly in the high latitude regions, caused by the collision of energetic charged particles with atoms in the high altitude atmosphere...

 are most common around L=6, can reach L=4 during moderate disturbances, and during the most severe geomagnetic storm

Geomagnetic storm

A geomagnetic storm is a temporary disturbance of the Earth's magnetosphere caused by a disturbance in the interplanetary medium. A geomagnetic storm is a major component of space weather and provides the input for many other components of space weather...

s, may approach L=2. The Van Allen radiation belt

Van Allen radiation belt

The Van Allen radiation belt is a torus of energetic charged particles around Earth, which is held in place by Earth's magnetic field. It is believed that most of the particles that form the belts come from solar wind, and other particles by cosmic rays. It is named after its discoverer, James...

s roughly correspond to L=1.5-2.5, and L=4-6. The plasmapause is typically around L=5.

L-shells on Jupiter

The Jovian magnetic field is the strongest planetary field in the solar system. Its magnetic field traps electrons with energies greater than 500 MeV The characteristic L-shells are L=6, where electron distribution undergoes a marked hardening (increase of energy), and L=20-50, where the electron energy decreases to the VHF regime and the magnetosphere eventually gives way to the solar wind. Because Jupiter's trapped electrons contain so much energy, they more easily diffuse across L-shells than trapped electrons in Earth's magnetic field. One consequence of this is a more continuous and smoothly-varying radio-spectrum emitted by trapped electrons in gyro-resonance

Electron cyclotron resonance

Electron cyclotron resonance is a phenomenon observed both in plasma physics and condensed matter physics. An electron in a static and uniform magnetic field will move in a circle due to the Lorentz force...

.

See also

• Earth's magnetic field
  Earth's magnetic field
  Earth's magnetic field is the magnetic field that extends from the Earth's inner core to where it meets the solar wind, a stream of energetic particles emanating from the Sun...
  
  
• Dipole model of the Earth's magnetic field
  Dipole model of the Earth's magnetic field
  The dipole model of the Earth's magnetic field is a first order approximation of the rather complex true Earth's magnetic field. Due to effects of the interplanetary magnetic field, and the solar wind, the dipole model is particularly inaccurate at high L-shells , but may be a good approximation...
  
  
• Guiding center
  Guiding center
  In many cases of practical interest, the motion in a magnetic field of an electrically charged particle can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point...
  
  
• Geomagnetic latitude
  Geomagnetic latitude
  Geomagnetic latitude is a parameter analogous to geographic latitude, except that bearing is with respect to the magnetic poles, as opposed to the geographic poles....
  
  
• International Geomagnetic Reference Field
• TEP
• World Magnetic Model
  World Magnetic Model
  The World Magnetic Model is a large spatial-scale representation of the Earth's magnetic field. It consists of a degree and order 12 spherical-harmonic expansion of the magnetic potential of the geomagnetic main field generated in the Earth’s core...
  
  

Other references

• Tascione, Thomas F. (1994), Introduction to the Space Environment (2nd ed.), Malabar, FL: Kreiger
• Margaret Kivelson and Christopher Russell (1995), Introduction to Space Physics, New York, NY: Cambridge University Press, pp. 166–167