
Lagrange multipliers on Banach spaces
Encyclopedia
In the field of calculus of variations
in mathematics
, the method of Lagrange multipliers on Banach spaces can be used to solve certain infinite-dimensional constrained
optimization problems
. The method is a generalization of the classical method of Lagrange multipliers
as used to find extrema of a function
of finitely many variables.
Banach space
s. Let U be an open subset
of X and let f : U → R be a continuously differentiable function
. Let g : U → Y be another continuously differentiable function, the constraint: the objective is to find the extremal points (maxima or minima) of f subject to the constraint that g is zero.
Suppose that u0 is a constrained extremum of f, i.e. an extremum of f on
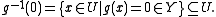
Suppose also that the Fréchet derivative
Dg(u0) : X → Y of g at u0 is a surjective linear map. Then there exists a Lagrange multiplier λ : Y → R in Y∗, the dual space
to Y, such that
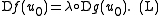
Since Df(u0) is an element of the dual space X∗, equation (L) can also be written as
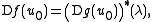
where (Dg(u0))∗(λ) is the pullback
of λ by Dg(u0), i.e. the action of the adjoint
map (Dg(u0))∗ on λ, as defined by
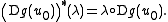
form shows that λ is the usual Lagrange multiplier vector; in the case m = n = 1, λ is the usual Lagrange multiplier, a real number.
Consider, for example, the Sobolev space
X = H01([−1, +1]; R) and the functional f : X → R given by
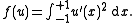
Without any constraint, the minimum value of f would be 0, attained by u0(x) = 0 for all x between −1 and +1. One could also consider the constrained optimization problem, to minimize f among all those u ∈ X such that the mean value of u is +1. In terms of the above theorem, the constraint g would be given by
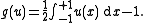
The method of Lagrange multipliers on Banach spaces is required in order to solve this problem.
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the method of Lagrange multipliers on Banach spaces can be used to solve certain infinite-dimensional constrained
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
optimization problems
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
. The method is a generalization of the classical method of Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
as used to find extrema of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of finitely many variables.
The Lagrange multiplier theorem for Banach spaces
Let X and Y be realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. Let U be an open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of X and let f : U → R be a continuously differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
. Let g : U → Y be another continuously differentiable function, the constraint: the objective is to find the extremal points (maxima or minima) of f subject to the constraint that g is zero.
Suppose that u0 is a constrained extremum of f, i.e. an extremum of f on
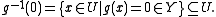
Suppose also that the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
Dg(u0) : X → Y of g at u0 is a surjective linear map. Then there exists a Lagrange multiplier λ : Y → R in Y∗, the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
to Y, such that
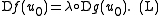
Since Df(u0) is an element of the dual space X∗, equation (L) can also be written as
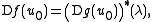
where (Dg(u0))∗(λ) is the pullback
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
of λ by Dg(u0), i.e. the action of the adjoint
Adjoint
In mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...
map (Dg(u0))∗ on λ, as defined by
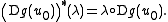
Connection to the finite-dimensional case
In the case that X and Y are both finite-dimensional (i.e. linearly isomorphic to Rm and Rn for some natural numbers m and n) then writing out equation (L) in matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form shows that λ is the usual Lagrange multiplier vector; in the case m = n = 1, λ is the usual Lagrange multiplier, a real number.
Application
In many optimization problems, one seeks to minimize a functional defined on an infinite-dimensional space such as a Banach space.Consider, for example, the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
X = H01([−1, +1]; R) and the functional f : X → R given by
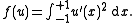
Without any constraint, the minimum value of f would be 0, attained by u0(x) = 0 for all x between −1 and +1. One could also consider the constrained optimization problem, to minimize f among all those u ∈ X such that the mean value of u is +1. In terms of the above theorem, the constraint g would be given by
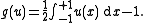
The method of Lagrange multipliers on Banach spaces is required in order to solve this problem.

