
Lagrange reversion theorem
Encyclopedia
In mathematics
, the Lagrange reversion theorem gives series
or formal power series
expansions of certain implicitly defined functions; indeed, of compositions with such functions.
Let v be a function of x and y in terms of another function f such that
Then for any function g,
for small y. If g is the identity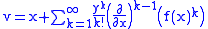
In 1770, Joseph Louis Lagrange
(1736–1813) published his power series solution of the implicit equation for v mentioned above. However, his solution used cumbersome series expansions of logarithms. In 1780, Pierre-Simon Laplace
(1749–1827) published a simpler proof of the theorem, which was based on relations between partial derivatives with respect to the variable x and the parameter y. Charles Hermite
(1822–1901) presented the most straightforward proof of the theorem by using contour integration.
Lagrange's reversion theorem is used to obtain numerical solutions to Kepler's equation
.

Writing the delta-function as an integral we have:
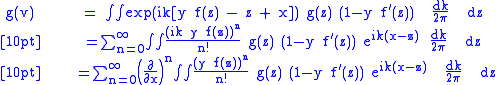
The integral over k then gives and we have:
and we have:

Rearranging the sum and cancelling then gives the result:
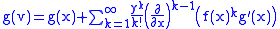
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lagrange reversion theorem gives series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
or formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
expansions of certain implicitly defined functions; indeed, of compositions with such functions.
Let v be a function of x and y in terms of another function f such that

Then for any function g,

for small y. If g is the identity
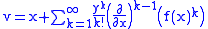
In 1770, Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
(1736–1813) published his power series solution of the implicit equation for v mentioned above. However, his solution used cumbersome series expansions of logarithms. In 1780, Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
(1749–1827) published a simpler proof of the theorem, which was based on relations between partial derivatives with respect to the variable x and the parameter y. Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
(1822–1901) presented the most straightforward proof of the theorem by using contour integration.
Lagrange's reversion theorem is used to obtain numerical solutions to Kepler's equation
Kepler's equation
Kepler's equation is M = E -\epsilon \cdot \sin E ,where M is the mean anomaly, E is the eccentric anomaly, and \displaystyle \epsilon is the eccentricity....
.
Simple proof
We start by writing:
Writing the delta-function as an integral we have:
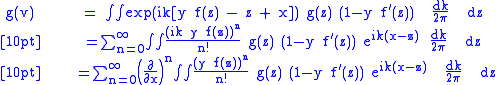
The integral over k then gives
 and we have:
and we have:
Rearranging the sum and cancelling then gives the result:
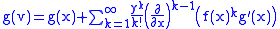
External links
- Lagrange Inversion [Reversion] Theorem on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Cornish–Fisher expansion, an application of the theorem
- Article on equation of timeEquation of timeThe equation of time is the difference between apparent solar time and mean solar time. At any given instant, this difference will be the same for every observer...
contains an application to Kepler's equation.

