
Lambda cube
Encyclopedia
In mathematical logic
and type theory
, the λ-cube is a framework for exploring the axes of refinement in Coquand
's calculus of constructions
, starting from the simply typed lambda calculus
as the vertex of a cube placed at the origin, and the calculus of constructions (higher order dependently-typed polymorphic lambda calculus) as its diametrically opposite vertex. Each axis of the cube represents a new form of abstraction:
All eight calculi include the most basic form of abstraction, terms depending on terms, ordinary functions as in the simply-typed lambda calculus. The richest calculus in the cube, with all three abstractions, is the calculus of constructions
. All eight calculi are strongly normalizing
.
Subtyping however is not represented in the cube, even though systems like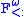 , known as higher-order bounded quantification, which combines subtyping and polymorphism are of practical interest, and can be further generalized to bounded type operators. Further extensions to
, known as higher-order bounded quantification, which combines subtyping and polymorphism are of practical interest, and can be further generalized to bounded type operators. Further extensions to 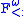 allow the definition of purely functional objects; these systems were generally developed after the lambda cube paper was published.
allow the definition of purely functional objects; these systems were generally developed after the lambda cube paper was published.
The idea of the cube is due to the mathematician Henk Barendregt
(1991). The framework of pure type system
s generalizes the lambda cube in the sense that all corners of the cube, as well as many other systems can be represented as instances of this general framework. This framework predates lambda cube a couple of years. In his 1991 paper, Barendregt also defines the corners of the cube in this framework.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, the λ-cube is a framework for exploring the axes of refinement in Coquand
Thierry Coquand
Thierry Coquand is a professor in computer science at the University of Gothenburg, Sweden. He is known for his work in constructive mathematics, especially the calculus of constructions. He received his Ph.D. under the supervision of Gérard Huet.- External links :*...
's calculus of constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
, starting from the simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
as the vertex of a cube placed at the origin, and the calculus of constructions (higher order dependently-typed polymorphic lambda calculus) as its diametrically opposite vertex. Each axis of the cube represents a new form of abstraction:
- Terms depending on types, or polymorphism. System FSystem FSystem F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
, aka second order lambda calculus, is obtained by imposing only this property. - Types depending on types, or type operators. Simply typed lambda-calculus with type operators, λω, is obtained by imposing only this property. Combined with System FSystem FSystem F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
it yields System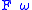 .
. - Types depending on terms, or dependent types. Imposing only this property yields λΠ, a type system closely related to LFLF (logical framework)In logic, a logical framework provides a means to define a logic as a signature in a higher-order type theory in such a way that provability of a formula in the original logic reduces to a type inhabitation problem in the framework type theory. This approach has been used successfully for ...
.
All eight calculi include the most basic form of abstraction, terms depending on terms, ordinary functions as in the simply-typed lambda calculus. The richest calculus in the cube, with all three abstractions, is the calculus of constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
. All eight calculi are strongly normalizing
Normalization property (lambda-calculus)
In mathematical logic and theoretical computer science, a rewrite system has the strong normalization property if every term is strongly normalizing; that is, if every sequence of rewrites eventually terminates to a term in normal form...
.
Subtyping however is not represented in the cube, even though systems like
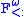 , known as higher-order bounded quantification, which combines subtyping and polymorphism are of practical interest, and can be further generalized to bounded type operators. Further extensions to
, known as higher-order bounded quantification, which combines subtyping and polymorphism are of practical interest, and can be further generalized to bounded type operators. Further extensions to 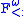 allow the definition of purely functional objects; these systems were generally developed after the lambda cube paper was published.
allow the definition of purely functional objects; these systems were generally developed after the lambda cube paper was published.The idea of the cube is due to the mathematician Henk Barendregt
Henk Barendregt
Hendrik Pieter Barendregt is a Dutch logician, known for his work in lambda calculus and type theory.Barendregt studied mathematical logic at Utrecht University, obtaining his Masters in 1968 and his Ph.D. in 1971, both cum laude, under Dirk van Dalen and Georg Kreisel...
(1991). The framework of pure type system
Pure type system
In the branches of mathematical logic known as proof theory and type theory, a pure type system , previously known as a generalized type system , is a form of typed lambda calculus that allows an arbitrary number of sorts and dependencies between any of these...
s generalizes the lambda cube in the sense that all corners of the cube, as well as many other systems can be represented as instances of this general framework. This framework predates lambda cube a couple of years. In his 1991 paper, Barendregt also defines the corners of the cube in this framework.
Further reading
- Simon Peyton Jones and Erik Meijer, 1997. Henk: A Typed Intermediate Language
External links
- Barendregt's Lambda Cube in the context of pure type systems by Roger Bishop Jones

