
Lami's theorem
Encyclopedia
In statics
, Lami's theorem is an equation relating the magnitudes of three coplanar, concurrent and non-collinear
forces, which keeps an object in static equilibrium, with the angles directly opposite to the corresponding forces. According to the theorem,
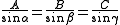
Lami's theorem is applied in static analysis of mechanical and structural systems. The theorem is named after Bernard Lamy
.
By the law of sines
,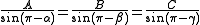
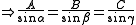
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
, Lami's theorem is an equation relating the magnitudes of three coplanar, concurrent and non-collinear
Coplanarity
In geometry, a set of points in space is coplanar if all the points lie in the same geometric plane. For example, three distinct points are always coplanar; but a fourth point or more added in space can exist in another plane, incoplanarly....
forces, which keeps an object in static equilibrium, with the angles directly opposite to the corresponding forces. According to the theorem,
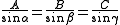
- where A, B and C are the magnitudes of three coplanar, concurrent and non-collinear forces, which keeps the object in static equilibrium, and
- α, β and γ are the angles directly opposite to the forces A, B and C respectively.
Lami's theorem is applied in static analysis of mechanical and structural systems. The theorem is named after Bernard Lamy
Bernard Lamy (mathematician)
Bernard Lamy was a French Oratorian mathematician and theologian.-Life:...
.
Proof of Lami's Theorem
Suppose there are three coplanar, concurrent and non-collinear forces, which keeps the object in static equilibrium. By the triangle law, we can re-construct the diagram as follow:By the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
,
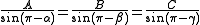
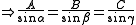
Further reading
- R.K. Bansal (2005). "A Textbook of Engineering Mechanics". Laxmi Publications. p. 4. ISBN 9788170083054.
- I.S. Gujral (2008). "Engineering Mechanics". Firewall Media. p. 10. ISBN 9788131802953

