
Landau's function
Encyclopedia
In mathematics, Landau's function g(n), named after Edmund Landau
, is defined for every natural number
n to be the largest order
of an element of the symmetric group
Sn. Equivalently, g(n) is the largest least common multiple
(lcm) of any partition of n, or the maximum number of times a permutation
of n elements can be recursively applied to itself before it returns to its starting sequence.
For instance, 5 = 2 + 3 and lcm(2,3) = 6. No other partition of 5 yields a bigger lcm, so g(5) = 6. An element of order 6 in the group S5 can be written in cycle notation as (1 2) (3 4 5).
The integer sequence
g(0) = 1, g(1) = 1, g(2) = 2, g(3) = 3, g(4) = 4, g(5) = 6, g(6) = 6, g(7) = 12, g(8) = 15, ... is named after Edmund Landau
, who proved in 1902 that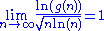
(where ln denotes the natural logarithm
).
The statement that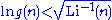
for all n, where Li−1 denotes the inverse of the logarithmic integral function
, is equivalent to the Riemann hypothesis
.
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
, is defined for every natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n to be the largest order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of an element of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn. Equivalently, g(n) is the largest least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
(lcm) of any partition of n, or the maximum number of times a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of n elements can be recursively applied to itself before it returns to its starting sequence.
For instance, 5 = 2 + 3 and lcm(2,3) = 6. No other partition of 5 yields a bigger lcm, so g(5) = 6. An element of order 6 in the group S5 can be written in cycle notation as (1 2) (3 4 5).
The integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
g(0) = 1, g(1) = 1, g(2) = 2, g(3) = 3, g(4) = 4, g(5) = 6, g(6) = 6, g(7) = 12, g(8) = 15, ... is named after Edmund Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
, who proved in 1902 that
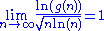
(where ln denotes the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
).
The statement that
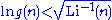
for all n, where Li−1 denotes the inverse of the logarithmic integral function
Logarithmic integral function
In mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...
, is equivalent to the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.

