Landau–Lifshitz–Gilbert equation
Encyclopedia
In physics, the Landau-Lifshitz-Gilbert equation , named for Lev Landau
and Evgeny Lifshitz
and T. L. Gilbert, is a name used for a differential equation describing the precessional motion of magnetization
M in a solid. It is a modification by Gilbert of the original equation of Landau and Lifshitz.
The various forms of the equation are commonly used in micromagnetics to model the effects of a magnetic field on ferromagnetic materials. In particular it can be used to model the behaviour of hard disk drives .
the precessional motion of magnetization
in a solid with an effective magnetic field 
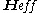and with damping. It is the ordinary differential equation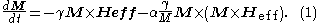
The constant
is the Landau-Lifshitz phenomenological damping parameter and depends on the solid, and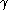 
is the electron gyromagnetic ratio.
Using the methods of irreversible thermodynamics, numerous authors have independently obtained the Landau-Lifshitz equation.
In irreversible thermodynamics, the thermodynamic forces are non-zero when the system is out of equilibrium. Here the thermodynamic force is the cross-product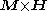
; hence only the vectors 
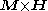(precession) and 
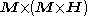(damping) are allowed in 
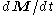. The result is the Landau-Lifshitz form.
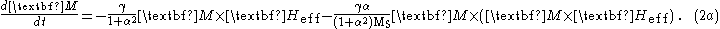
Surprisingly this can be transformed by a somewhat cumbersome calculation into an equivalent expression where the additional complications seem to have been transformed away,
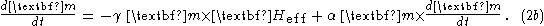
Here we have used the identification
Now the final summand, containing the damping, looks simpler.
The LL-E above, (1), works fairly well when the damping is small, but fails for large damping (α comparable to or greater than unity). This problem was fixed by Gilbert through his modification, (2a), or equivalently (2b).
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
and Evgeny Lifshitz
Evgeny Lifshitz
Evgeny Mikhailovich Lifshitz was a leading Soviet physicist of Jewish origin and the brother of physicist Ilya Mikhailovich Lifshitz. Lifshitz is well known in general relativity for coauthoring the BKL conjecture concerning the nature of a generic curvature...
and T. L. Gilbert, is a name used for a differential equation describing the precessional motion of magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
M in a solid. It is a modification by Gilbert of the original equation of Landau and Lifshitz.
The various forms of the equation are commonly used in micromagnetics to model the effects of a magnetic field on ferromagnetic materials. In particular it can be used to model the behaviour of hard disk drives .
Landau-Lifshitz ordinary differential equation
The LL equation was introduced by to modelthe precessional motion of magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
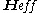in a solid with an effective magnetic field and with damping. It is the ordinary differential equation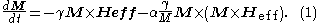The constant
is the Landau-Lifshitz phenomenological damping parameter and depends on the solid, and 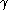is the electron gyromagnetic ratio.Using the methods of irreversible thermodynamics, numerous authors have independently obtained the Landau-Lifshitz equation.
In irreversible thermodynamics, the thermodynamic forces are non-zero when the system is out of equilibrium. Here the thermodynamic force is the cross-product
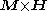; hence only the vectors 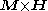(precession) and 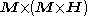(damping) are allowed in 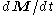. The result is the Landau-Lifshitz form.Landau-Lifshitz-Gilbert equation
In 1955 Gilbert replaced the damping term, by introducing some kind of viscous force. This led to the following, obviously even more complicating expression, known as the Landau-Lifshitz-Gilbert equation (LLG-E):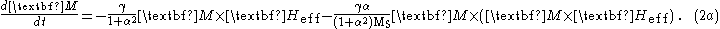Surprisingly this can be transformed by a somewhat cumbersome calculation into an equivalent expression where the additional complications seem to have been transformed away,
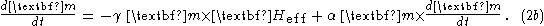
Here we have used the identification
Now the final summand, containing the damping, looks simpler.The LL-E above, (1), works fairly well when the damping is small, but fails for large damping (α comparable to or greater than unity). This problem was fixed by Gilbert through his modification, (2a), or equivalently (2b).