Landau–Zener formula
Encyclopedia
The Landau–Zener formula is an analytic solution to the equations of motion governing the transition dynamics of a 2-level
quantum mechanical
system, with a time-dependent Hamiltonian
varying such that the energy separation of the two states is a linear function of time. The formula, giving the probability of a diabatic
(not adiabatic
) transition between the two energy states, was published separately by Lev Landau
, Clarence Zener
, Ernst Stueckelberg
, and Ettore Majorana
, in 1932.
If the system starts, in the infinite past, in the lower energy eigenstate, we wish to calculate the probability of finding the system in the upper energy eigenstate in the infinite future (a so-called Landau–Zener transition). For infinitely slow variation of the energy difference (that is, a Landau–Zener velocity of zero), the adiabatic theorem
tells us that no such transition will take place, as the system will always be in an instantaneous eigenstate of the Hamiltonian at that moment in time. At non-zero velocities, transitions occur with probability as described by the Landau–Zener formula.
s and external electric
and magnetic
fields. In order that the equations of motion for the system might be solved analytically, a set of simplifications are made, known collectively as the Landau–Zener approximation. The simplifications are as follows:
The first simplification makes this a semi-classical treatment. In the case of an atom in a magnetic field, the field strength becomes a classical variable which can be precisely measured during the transition. This requirement is quite restrictive as a linear change will not, in general, be the optimal profile to achieve the desired transition probability.
The second simplification allows us to make the substitution
where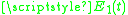
and 
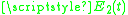are the energies of the two states at time 
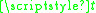, given by the diagonal elements of the Hamiltonian matrix, and 
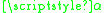is a constant. For the case of an atom in a magnetic field this corresponds to a linear change in magnetic field. For a linear Zeeman shift
this follows directly from point 1.
The final simplification requires that the time–dependent perturbation does not
couple the diabatic states; rather, the coupling must be due to a static deviation from
a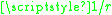
coulomb potential, commonly described by a quantum defect
.
.
The key figure of merit in this approach is the Landau–Zener velocity:
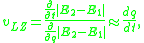
where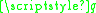
is the perturbation variable (electric or magnetic field, molecular bond-length, or any other perturbation to the system), and 
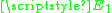and 
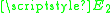are the energies of the two diabatic (crossing) states. A large 
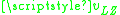results in a large diabatic transition probability and vice versa.
Using the Landau–Zener formula the probability,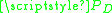
, of a diabatic transition is given by
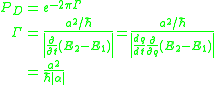
The quantity
is the off-diagonal element of the two-level system's Hamiltonian coupling the bases, and as such it is half the distance between the two unperturbed eigenenergies at the avoided crossing, when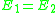 
.
(formulated by Sinitsyn and rigorously proved by Volkov and Ostrovsky)
Several classes of completely solvable multistate Landau–Zener models have been identified and studied, including:
Exact results in multistate Landau–Zener theory (no-go theorem
and BE-formula) can be applied to models of a Landau-Zener system coupled to oscillator or spin baths. They provide exact expressions for transition probabilities averaged over final bath states if the evolution begins from the ground state at zero temperature.
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
system, with a time-dependent Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
varying such that the energy separation of the two states is a linear function of time. The formula, giving the probability of a diabatic
Diabatic
A diabatic process is one in which heat transfer takes place, which is the opposite of an adiabatic process. In quantum chemistry, the potential energy surfaces are obtained within the adiabatic or Born-Oppenheimer approximation...
(not adiabatic
Adiabatic theorem
The adiabatic theorem is an important concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock , can be stated as follows:...
) transition between the two energy states, was published separately by Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
, Clarence Zener
Clarence Zener
Clarence Melvin Zener was the American physicist who first described the property concerning the breakdown of electrical insulators. These findings were later exploited by Bell Labs in the development of the Zener diode, which was duly named after him...
, Ernst Stueckelberg
Ernst Stueckelberg
Ernst Carl Gerlach Stueckelberg was a Swiss mathematician and physicist.- Career :In 1927 Stueckelberg got his Ph. D. at the University of Basel under August Hagenbach...
, and Ettore Majorana
Ettore Majorana
Ettore Majorana was an Italian theoretical physicist who began work on neutrino masses. He disappeared suddenly in mysterious circumstances. He is noted for the eponymous Majorana equation and for Majorana fermions.-Gifted in mathematics:Majorana was born in Catania, Sicily...
, in 1932.
If the system starts, in the infinite past, in the lower energy eigenstate, we wish to calculate the probability of finding the system in the upper energy eigenstate in the infinite future (a so-called Landau–Zener transition). For infinitely slow variation of the energy difference (that is, a Landau–Zener velocity of zero), the adiabatic theorem
Adiabatic theorem
The adiabatic theorem is an important concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock , can be stated as follows:...
tells us that no such transition will take place, as the system will always be in an instantaneous eigenstate of the Hamiltonian at that moment in time. At non-zero velocities, transitions occur with probability as described by the Landau–Zener formula.
Landau–Zener approximation
Such transitions occur between states of the entire system, hence any description of the system must include all external influences, including collisionCollision
A collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
s and external electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
fields. In order that the equations of motion for the system might be solved analytically, a set of simplifications are made, known collectively as the Landau–Zener approximation. The simplifications are as follows:
- The perturbation parameter in the Hamiltonian is a known, linear function of time
- The energy separation of the diabatic states varies linearly with time
- The coupling in the diabatic Hamiltonian matrix is independent of time
The first simplification makes this a semi-classical treatment. In the case of an atom in a magnetic field, the field strength becomes a classical variable which can be precisely measured during the transition. This requirement is quite restrictive as a linear change will not, in general, be the optimal profile to achieve the desired transition probability.
The second simplification allows us to make the substitution
where
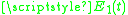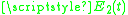and are the energies of the two states at time 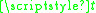, given by the diagonal elements of the Hamiltonian matrix, and 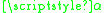is a constant. For the case of an atom in a magnetic field this corresponds to a linear change in magnetic field. For a linear Zeeman shiftZeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
this follows directly from point 1.
The final simplification requires that the time–dependent perturbation does not
couple the diabatic states; rather, the coupling must be due to a static deviation from
a
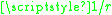coulomb potential, commonly described by a quantum defectQuantum defect
The term quantum defect is ambiguous. Various meanings are discussed below. Characteristic is that the defect deals with the loss on the smallest energy scale of light: that of the quantum.-Quantum defect in laser science:...
.
The Landau–Zener formula
The details of Zener's solution are somewhat opaque, relying on a set of substitutions to put the equation of motion into the form of the Weber equation and using the known solution. A more transparent solution is provided by Wittig using contour integrationMethods of contour integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
.
The key figure of merit in this approach is the Landau–Zener velocity:
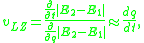
where
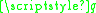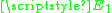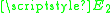is the perturbation variable (electric or magnetic field, molecular bond-length, or any other perturbation to the system), and and are the energies of the two diabatic (crossing) states. A large 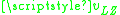results in a large diabatic transition probability and vice versa.Using the Landau–Zener formula the probability,
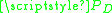, of a diabatic transition is given by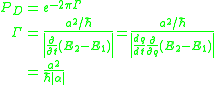The quantity
is the off-diagonal element of the two-level system's Hamiltonian coupling the bases, and as such it is half the distance between the two unperturbed eigenenergies at the avoided crossing, when 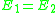.Multistate Landau–Zener problem
The simplest generalization of the two-state Landau–Zener model is a multistate system with the Hamiltonian of the form H(t)=A+Bt, where A and B are Hermitian NxN matrices with constant elements. An important feature of all such models is the existence of exact theorems that provide analytical expressions for special elements of the scattering matrix. These include the Brundobler–Elser formula (noticed by Brundobler and Elser in numerical simulations and rigorously proved by Dobrescu and Sinitsyn , following the contribution of Volkov and Ostrovsky) and the no-go theoremNo-go theorem
In theoretical physics, a no-go theorem is a theorem that states that a particular situation is not physically possible.-Examples of no-go theorems:* Bell's theorem* Coleman–Mandula theorem* Haag-Lopuszanski-Sohnius theorem* Earnshaw's theorem...
(formulated by Sinitsyn and rigorously proved by Volkov and Ostrovsky)
Several classes of completely solvable multistate Landau–Zener models have been identified and studied, including:
- Demkov–Osherov model
- Generalized bow-tie model
- Reducible multistate Landau–Zener models
- Landau–Zener transitions in a linear chain
Noise in the Landau–Zener problem
Applications of the Landau–Zener solution to the problems of quantum state preparation and manipulation with discrete degrees of freedom stimulated the study of noise and decoherence effects on the transition probability in a driven two-state system. Several compact analytical results have been derived to describe these effects, including the Kayanuma formula for a strong diagonal noise, and Pokrovsky–Sinitsyn formula for the coupling to a fast colored noise with off-diagonal components. The effects of nuclear spin bath and heat bath coupling on the Landau–Zener process were explored by Sinitsyn and Prokof'ev and Pokrovsky and Sun, respectively.Exact results in multistate Landau–Zener theory (no-go theorem
No-go theorem
In theoretical physics, a no-go theorem is a theorem that states that a particular situation is not physically possible.-Examples of no-go theorems:* Bell's theorem* Coleman–Mandula theorem* Haag-Lopuszanski-Sohnius theorem* Earnshaw's theorem...
and BE-formula) can be applied to models of a Landau-Zener system coupled to oscillator or spin baths. They provide exact expressions for transition probabilities averaged over final bath states if the evolution begins from the ground state at zero temperature.