Laplacian smoothing
Encyclopedia
Laplacian smoothing is an algorithm to smooth
a polygonal mesh
. For each vertex in a mesh, a new position is chosen based on local information (such as the position of neighbors) and the vertex is moved there. In the case that a mesh is topologically a rectangular grid (that is, each internal vertex is connected to four neighbors) then this operation produces the Laplacian of the mesh.
More formally, the smoothing operation may be described per-vertex as:
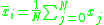
Where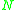
is the number of adjacent vertices to node 
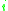and 
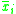is the new position for node 
.
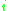Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
a polygonal mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
. For each vertex in a mesh, a new position is chosen based on local information (such as the position of neighbors) and the vertex is moved there. In the case that a mesh is topologically a rectangular grid (that is, each internal vertex is connected to four neighbors) then this operation produces the Laplacian of the mesh.
More formally, the smoothing operation may be described per-vertex as:
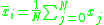
Where
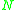is the number of adjacent vertices to node 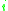and 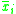is the new position for node .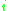