Lawvere theory
Encyclopedia
In category theory
, a Lawvere theory (named after American
mathematician
William Lawvere
) is a category
which can be considered a categorical counterpart of the notion of an equational theory.
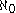be a skeleton
of the category FinSet
of finite sets and function
s. Formally, a Lawvere theory consists of a small category L with (strictly associative
) finite product
s and a strict identity-on-objects functor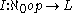
preserving finite products.
A model of a Lawvere theory in a category C with finite products is a finite-product preserving functor .
Lawvere theories together with maps between them form the category Law.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a Lawvere theory (named after American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
William Lawvere
William Lawvere
Francis William Lawvere is a mathematician known for his work in category theory, topos theory and the philosophy of mathematics.-Biography:...
) is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
which can be considered a categorical counterpart of the notion of an equational theory.
Definition
Let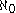 be a skeletonSkeleton (category theory)
In mathematics, a skeleton of a category is a subcategory which, roughly speaking, does not contain any extraneous isomorphisms. In a certain sense, the skeleton of a category is the "smallest" equivalent category which captures all "categorical properties". In fact, two categories are equivalent...
of the category FinSet
FinSet
In the mathematical field of category theory, FinSet is the category whose objects are all finite sets and whose morphisms are all functions between them...
of finite sets and function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. Formally, a Lawvere theory consists of a small category L with (strictly associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
) finite product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
s and a strict identity-on-objects functor
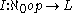preserving finite products.A model of a Lawvere theory in a category C with finite products is a finite-product preserving functor .
Category of Lawvere theories
A map between Lawvere theories (L,I) and (L′,I′) is a finite-product preserving functor which commutes with I and I′. Such a map is commonly seen as an interpretation of (L,I) in (L′,I′).Lawvere theories together with maps between them form the category Law.