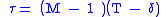Leaky bucket
Encyclopedia
The leaky bucket is an algorithm
used in packet switched computer network
s and telecommunications networks
to check that data transmission
s conform to defined limits on bandwidth
and burstiness
(a measure of the unevenness or variations in the traffic
flow). The leaky bucket algorithm is also used in leaky bucket counters, e.g. to detect when the average or peak rate of random or stochastic
events or stochastic processes exceed defined limits.
The Leaky Bucket Algorithm is based on an analogy
of a bucket
(figure 1) that has a hole in the bottom through which any water it contains will leak away at a constant rate, until or unless it is empty. Water can be added intermittently, i.e. in bursts, but if too much is added at once, or it is added at too high an average rate, the water will exceed the capacity
of the bucket, which will overflow.
There are actually two different methods of applying this analogy described in the literature. These give what appear to be two different algorithms, both of which are referred to as the leaky bucket algorithm. This has resulted in confusion about what the leaky bucket algorithm is and what its properties are.
In one version, the analogue of the bucket is a counter or variable, separate from the flow of traffic, and is used only to check that traffic conforms to the limits, i.e. the analogue of the water is brought to the bucket by the traffic and added to it so that the level of water in the bucket indicates conformance to the rate and burstiness limits. This version is referred to here as the leaky bucket as a meter. In the second version, the traffic passes through a queue that is the analogue of the bucket, i.e. the traffic is the analogue of the water passing through the bucket. This version is referred to here as the leaky bucket as a queue. The leaky bucket as a meter is equivalent to (a mirror image of) the token bucket
algorithm, and given the same parameters will see the same traffic as conforming or nonconforming. The leaky bucket as a queue can be seen as a special case of the leaky bucket as a meter.
A version of the leaky bucket algorithm, the Generic Cell Rate Algorithm
, is recommended for Asynchronous Transfer Mode
networks in Usage/Network Parameter Control at User–Network Interfaces or Inter-Network Interfaces or Network-Network Interfaces
. The Generic Cell Rate Algorithm, or an equivalent, may also be used to control transmissions by a Network Interface Card onto an ATM network (i.e. on the user side of the User-Network Interface).
is credited with the original description of the leaky bucket algorithm and describes it as follows: “A counter associated with each user transmitting on a connection is incremented whenever the user sends a packet and is decremented periodically. If the counter exceeds a threshold upon being incremented, the network discards the packet. The user specifies the rate at which the counter is decremented (this determines the average bandwidth) and the value of the threshold (a measure of burstiness)”. The bucket (analogous to the counter) is in this case used as a meter to test the conformance of packets, rather than as a queue to directly control them.
Another version of what is essentially the same meter version of the algorithm, the Generic Cell Rate Algorithm
, is described by the ITU-T
in recommendation I.371. and in the ATM Forum
’s UNI Specification. The description, in which the term cell is equivalent to packet in Turner's description is given by the ITU-T as follows: “The continuous-state leaky bucket can be viewed as a finite capacity bucket whose real-valued content drains out at a continuous rate of 1 unit of content per time unit and whose content is increased by the increment T for each conforming cell... If at a cell arrival the content of the bucket is less than or equal to the limit value τ, then the cell is conforming; otherwise, the cell is non-conforming. The capacity of the bucket (the upper bound of the counter) is (T + τ)”.
David E. McDysan and Darrel L. Spohn provide a commentary on the description given by the ITU-T/ATM Forum. In this they state “In the leaky bucket analogy, the [ATM] cells do not actually flow through the bucket; only the check for conforming admission does”. However, uncommonly in the descriptions in the literature, McDysan and Spohn also refer to the leaky bucket algorithm as a queue, going on “Note that one implementation of traffic shaping is to actually have the cells flow through the bucket”.
In describing the operation of the ITU-T's version of the algorithm, McDysan and Spohn invoke a “notion commonly employed in queueing theory
of a fictional ‘gremlin’”. This gremlin inspects the level in the bucket and takes action if the level is above the limit value τ : in policing (figure 2), it pulls open a trap door, which causes the packet to be dropped and stops its water from entering the bucket; in shaping (figure 3), it pushes up a flap, which delays the packet and prevents it from delivering its water, until the water level in the bucket falls below τ.
The difference between the descriptions given by Turner and the ITU-T/ATM Forum is that Turner's is specific to traffic policing, whereas the ITU-T/ATM Forum's is applicable to both traffic policing and traffic shaping. Also, Turner does not state that the contents of the counter should only be affected by conforming packets, and should only be incremented when this would not cause it to exceed the threshold, i.e. Turner does not explicitly state that the bucket’s capacity or counter's maximum value is finite. To make Turner’s description clearly aligned with ITU-T, the statement “If the counter exceeds a threshold upon being incremented, the network discards the packet” would have to be changed to something like “If the counter would exceed a threshold upon being incremented, the network discards the packet and the counter is not incremented”.
In fairness, the description given by Turner is in terms of a traffic policing function, where overzealousness in limiting a connection containing nonconforming packets may not be an issue. Indeed, in some contexts, such as Variable bitrate
(VBR) transmissions, the loss of any one packet may corrupt the entirety of a higher layer message, e.g. an OSI Network Layer PDU. In which case, discarding all the following packets of that corrupted PDU sheds an unnecessary network load. However, it would be entirely unacceptable in traffic shaping for a packet that fails the conformance test to affect how long before conformance can next occur, i.e. if the act of testing would change how long the packet has to wait.
Neither Turner nor the ITU-T addresses the issue of variable length packets. To be fair again, the description according to the ITU-T is for ATM cells, which are fixed length packets, and Turner does not specifically exclude variable length packets. In both cases, if the amount by which the bucket content or counter is incremented for a conforming packet is proportional to the packet length, they will both account for the length and allow the algorithm to limit the bandwidth of the traffic explicitly rather than limiting the packet rate.
or traffic policing
. For example, in ATM networks, in the form of the Generic Cell Rate Algorithm, it is used to compare the bandwidth and burstiness of traffic on a Virtual Channel or Virtual Path against the specified limits. In traffic policing, nonconforming cells may be discarded (dropped) or may be reduced in priority (for downstream traffic management functions to drop if there is congestion). In traffic shaping, cells are delayed until they conform. Traffic policing and traffic shaping are commonly used in UPC/NPC to protect the network against excess or excessively bursty traffic, see bandwidth management
and congestion avoidance. Traffic shaping is commonly used in the network interfaces in hosts to prevent transmissions being discarded by traffic management functions in the network.
The leaky bucket algorithm as a meter can also be used in a leaky bucket counter to measure the rate of random or stochastic processes. A Leaky bucket counter can be used to detect when the average or peak rate of events increases above some, acceptable, background level, i.e. when the bucket overflows. However, events that do not cause an overflow, i.e. have sufficiently low rates and are well distributed over time, can be ignored. For example, such a leaky bucket counter can be used to detect when there is a sudden burst of correctable memory errors or when there has been a gradual, but significant, increase in the average rate, which may indicate an impending failure, etc.
The use of the leaky bucket algorithm in a leaky bucket counter is similar to that in traffic management, in that it is used as a meter. Essentially, the events replace the packets in the description, with each event causing a quantity of water to be added to the bucket. If the bucket would overflow, as a result of the event, then the event should trigger the action associated with an out of limits event. Some implementations seem to parallel Turner's description, in that there is no explicit limit on the maximum value that the counter may take, implying that once the counter has exceeded the threshold, it may not return to its previous state until a period significantly greater than the equivalent of the emission interval has passed, which may be increased by what would otherwise be conforming events. Other implementations may, however, not increment the counter while it is overflowed, allowing it to correctly determine whether following events conform or not.
The bandwidth limit and burstiness limit for the connection may be specified in a traffic contract
. A bandwidth limit may be specified as a packet or frame rate, a byte or bit rate
, or as an emission interval between the packets. A limit on burstiness may be specified as a jitter
or delay variation tolerance, or as a maximum burst size (MBS).
Multiple sets of contract parameters can be applied concurrently to a connection using multiple instances of the leaky bucket algorithm, each of which may take a bandwidth and a burstiness limit: see Dual Leaky Bucket Controller.
Consider a bucket that is exactly filled to the top by preceding traffic, i.e. when the maximum permitted burstiness has already occurred. The minimum interval before the next packet can conform is then the time it takes for the bucket to leak exactly the amount of water delivered by a packet, and if a packet is tested and conforms at that time, this will exactly fill the bucket once more. Thus, once the bucket is filled, the maximum rate that packets can conform is with this interval between each packet.
Turner refers to this rate as the average, implying that its inverse is the average interval. There is, however, some ambiguity in what the average rate and interval are. Since, packets can arrive at any lower rate, this is an upper bound, rather than a fixed value, so it could at best be called the maximum for the average rate. Also, during the time the maximum burstiness occurs, packets can arrive with smaller intervals and thus a higher rate than this. So, for any period less than infinity, the actual average rate can be (but isn’t necessarily) greater than this and the average interval can be (but isn’t necessarily) less than the emission interval. Hence, because of this ambiguity, the term emission interval is used hereafter. However, it is still true that the minimum value that the long term average interval can take tends to be the emission interval.
For variable length packets, where the amount added to the bucket is proportional to the packet length, the maximum rate at which they can conform varies according to their length: the amount that the bucket must have leaked from full for a packet to conform is the amount the packet will add, and if this is proportional to the packet length, so is the interval between it and the preceding packet that filled the bucket. Hence, it is not possible to specify a specific emission interval for variable length packets, and the bandwidth limit has to be specified explicitly, in bits or bytes per second.
The ITU-T define a limit value, τ that is T less than the capacity of the bucket. This limit values specifies how much earlier a packet can arrive than it would normally be expected if the packets were arriving with exactly the emission interval between them.
Imagine the following situation: A bucket leaks at 1 unit of water per second, so the limit value, τ and the amount of water added by a packet, T, are effectively in units of seconds. This bucket starts off empty, so the first packet to arrive must conform. The bucket then becomes exactly full after a number of conforming packets, N, have arrived in the minimum possible time to conform. For the last (Nth) packet to conform, the bucket must have leaked enough of the water from the preceding N – 1 packets ((N – 1) * T seconds worth) for it to be exactly at the limit value τ at this time. Hence, the water leaked is (N– 1)T – τ, which because the leak is one unit per second, took exactly (N– 1)T – τ seconds to leak. Thus the shortest time in which all N packets can arrive and conform is (N– 1)T – τ seconds, which is exactly τ less than the time it would have taken if the packets had been arriving at exactly the emission interval.
Since the limit value τ defines how much earlier a packet can arrive than would be expected, it is the limit on the difference between the maximum and minimum delays from the source (assuming the packets are generated with no jitter) to the point where the conformance test is being made. Hence, the use of the term Cell Delay Variation tolerance (CDVt) for this parameter in ATM.
As an example, a possible source of delay variation is where a number of connections (streams of packets) are multiplexed together at the output of a switch. Assuming that the sum of the bandwidths of these connections is less than that of the output, all of the packets that arrive can be transmitted, eventually. However, if their arrivals are independent, e.g. because they arrive at different inputs of the switch, then several may arrive at or nearly at the same time. Since the output can only transmit one packet at a time, the others must be queued in a buffer until it is their turn to be transmitted. This buffer then introduces an additional delay between a packet arriving at an input and being transmitted by the output, and this delay varies, depending on how many other packets are already queued in the buffer. A similar situation can occur at the output of a host (in the NIC) when multiple packets have the same or similar release times, and this delay can usually be modelled as a delay in a virtual output buffer.
For variable length packets, where the amount of water added by a given packet is proportional to its length, τ can’t be seen as a limit on how full the bucket can be, as this varies depending on the packet size. However, the time it takes to drain from this level to empty is still how much earlier a packet can arrive than is expected, when packets are transmitted at the bandwidth limit. Thus, it is still the maximum variation in transfer delay to the point where the conformance test is being applied that can be tolerated, and thus the tolerance on maximum delay variation.
If the limit value is large enough, then several packets can arrive back-to-back and still conform: if the bucket starts from empty, the first packet to arrive will add T, but if, by the time the next packet arrives, the contents is below τ, this will also conform. Assuming that each packet takes δ to arrive at the line rate, then if τ (expressed as the time it takes the bucket to empty from the limit value) is equal to or greater than 'the emission interval less the minimum interarrival time, T – δ, the second packet will conform even if it arrives back-to-back with the first. Similarly, if τ is equal to or greater than (T – δ) × 2, then 3 packets can arrive back-to-back, etc.
The maximum size of this burst, M, can be calculated from the emission interval, T; the maximum jitter tolerance, τ; and the time taken to transmit/receive a packet, δ, as follows:
Equally, the minimum value of jitter tolerance τ that gives a specific MBS can be calculated from the MBS as follows:
For variable length packets, the maximum burst size will depend on the lengths of the packets in the burst and there is no single value for the maximum burst size. However, it is possible to specify the total burst length in bytes, from the byte rate of the input stream, the equivalent byte rate of the leak, and the bucket depth.
algorithm. However, the above concept of operation for the leaky bucket as a meter may be directly compared with the token bucket algorithm
, the description of which is given in that article as the following:
This can be compared with the concept of operation, repeated from above:
As can be seen, these two descriptions are essentially mirror images of one another: one adds something to the bucket on a regular basis and takes something away for conforming packets down to a limit of zero; the other takes away regularly and adds for conforming packets up to a limit of the bucket's capacity. It would also be perfectly possible to describe the process in terms of adding tokens or subtracting water for conforming packets as long as the regular process complements this, at which point it would become impossible to tell which was which: is an implementation that removes tokens regularly and adds tokens for a conforming packet an implementation of the leaky bucket or of the token bucket? In fact it is both, as these are the same basic algorithm described differently. This explains why, given equivalent parameters, the two algorithms will see exactly the same packets as conforming or nonconforming.
The differences in the properties and performance of implementations of the leaky and token bucket algorithms thus result entirely form the differences in the implementations, i.e. they do not stem from differences in the underling algorithms.
The points to note are that the leaky bucket algorithm, when used as a meter, can allow a conforming output packet stream with jitter or burstiness, can be used in traffic policing as well as shaping, and can be implemented for variable length packets.
, in his book Computer Networks as “The leaky bucket consists of a finite queue. When a packet arrives, if there is room on the queue it is appended to the queue; otherwise it is discarded. At every clock tick one packet is transmitted (unless the queue is empty)”.
As can be seen this implementation is restricted in that the packets are only ever transmitted at a fixed rate. To underline this, Tanenbaum also states that “The leaky bucket algorithm enforces a rigid output pattern at the average rate, no matter how bursty the [input] traffic is”. An implementation of the leaky bucket as a queue is therefore always a form of traffic shaping function.
A further restriction is that the leaky bucket as a queue traffic shaping function only transmits packets on the ticks; hence, if it is used within a network, equivalent to UPC and NPC, it also imposes a fixed phase on the onward transmission of packets. Perversely, in the context of the transfer delay, this imposition of a fixed phase that may be different from that of an otherwise conforming input packet stream, constitutes a delay variation and hence a jitter.
Limiting variable length packets using the leaky bucket algorithm as a queue is significantly more complicated than it is for fixed length packets. Tanenbaum gives a description of a “byte-counting” leaky bucket for variable length packets as follows: “At each tick, a counter is initialized to n. If the first packet on the queue has fewer bytes than the current value of the counter, it is transmitted, and the counter is decremented by that number of bytes. Additional packets may also be sent, as long as the counter is high enough. When the counter drops below the length of the next packet on the queue, transmission stops until the next tick, at which time the residual byte count is reset [to n] and the flow can continue”.
traffic to a specified bandwidth with no jitter in the output. It may be used within the network, e.g. as part of bandwidth management, etc., but is more appropriate to traffic shaping in the network interfaces of hosts.
The bandwidth limit for the connection may be specified in a traffic contract
. A bandwidth limit may be specified as a packet or frame rate, a byte or bit rate
, or as an emission interval between the packets.
Imagine a traffic shaping function for fixed length packets that is implemented using a fixed length queue, forming a delay element, which is serviced using a leaky bucket as a meter. Imagine also that the bucket in this meter has a depth equal to the amount added by a packet, i.e. has a limit value, τ, of zero. However, the conformance test is only performed at intervals of the emission interval, when the packet at the head of the queue is transmitted and its water is added. This water then leaks away during the next emission interval, allowing the next packet to conform then or at some subsequent emission interval. The service function can also be viewed in terms of a token bucket with the same depth, where enough tokens for one packet are added over the emission interval. This implementation will then receive packets with a bursty arrival pattern (limited by the queue depth) and transmit them on at intervals that are always exact (integral) multiples of the emission interval.
However, the implementation of the leaky bucket as a meter (or token bucket) in a traffic shaping function described above is an exact equivalent to the description of the leaky bucket as a queue: the delay element of the meter version is the bucket of the queue version; the bucket of the meter version is the process that services the queue, and the leak is such that the emission interval is the same as the tick interval. Therefore for fixed length packets, the implementation of the leaky bucket as a queue is of a special case of a traffic shaping function using a leaky bucket (or token bucket) as a meter in which the limit value, τ, is zero and the process is performed at the lowest possible rate.
The leaky bucket as a queue for variable packet lengths can also be described as equivalent to a special case of the leaky bucket as a meter. The suggested implementation can, like the fixed length implementation, be seen as traffic shaping function in which the queue is a delay element, rather than the bucket, and the function that services the queue is, in this case, explicitly given as a token bucket: it is decremented for conforming packets and incremented at a fixed rate. Hence, as the leaky bucket as a meter and token bucket are equivalent, the leaky bucket as a queue for variable packet lengths is also a special case of a traffic shaping function using a leaky bucket (or token bucket) as a meter.
There is an interesting consequence of seeing the leaky bucket as a queue for variable packet lengths as a specific implementation of the token bucket or leaky bucket as a meter in traffic shaping. This is that the bucket of the meter has a depth, n, and, as is always the case with the token bucket, this depth determines the burstiness of the output traffic (perhaps in relation to the average or minimum number of tokens required by the packets). Hence, it is possible to quantify the burstiness of the output of this "byte counting" leaky bucket as a meter, unless all packets are of the maximum length when it becomes pointless. However, this ability to define a burstiness for the output is in direct contradiction to the statement that the leaky bucket (as a queue) necessarily gives an output with a rigid rate, no matter how bursty the input.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
used in packet switched computer network
Computer network
A computer network, often simply referred to as a network, is a collection of hardware components and computers interconnected by communication channels that allow sharing of resources and information....
s and telecommunications networks
Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
to check that data transmission
Data transmission
Data transmission, digital transmission, or digital communications is the physical transfer of data over a point-to-point or point-to-multipoint communication channel. Examples of such channels are copper wires, optical fibres, wireless communication channels, and storage media...
s conform to defined limits on bandwidth
Bandwidth (computing)
In computer networking and computer science, bandwidth, network bandwidth, data bandwidth, or digital bandwidth is a measure of available or consumed data communication resources expressed in bits/second or multiples of it .Note that in textbooks on wireless communications, modem data transmission,...
and burstiness
Burst transmission
In telecommunication, the term burst transmission or data burst has the following meanings:# Any relatively high-bandwidth transmission over a short period of time...
(a measure of the unevenness or variations in the traffic
Network traffic
Network traffic is data in a network. In computer networks, the data is encapsulated in packets.*Network traffic control*Network traffic measurement*Network traffic simulation...
flow). The leaky bucket algorithm is also used in leaky bucket counters, e.g. to detect when the average or peak rate of random or stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
events or stochastic processes exceed defined limits.
The Leaky Bucket Algorithm is based on an analogy
Analogy
Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...
of a bucket
Bucket
A bucket, also called a pail, is typically a watertight, vertical cylinder or truncated cone, with an open top and a flat bottom, usually attached to a semicircular carrying handle called the bail. A pail can have an open top or can have a lid....
(figure 1) that has a hole in the bottom through which any water it contains will leak away at a constant rate, until or unless it is empty. Water can be added intermittently, i.e. in bursts, but if too much is added at once, or it is added at too high an average rate, the water will exceed the capacity
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of the bucket, which will overflow.
There are actually two different methods of applying this analogy described in the literature. These give what appear to be two different algorithms, both of which are referred to as the leaky bucket algorithm. This has resulted in confusion about what the leaky bucket algorithm is and what its properties are.
In one version, the analogue of the bucket is a counter or variable, separate from the flow of traffic, and is used only to check that traffic conforms to the limits, i.e. the analogue of the water is brought to the bucket by the traffic and added to it so that the level of water in the bucket indicates conformance to the rate and burstiness limits. This version is referred to here as the leaky bucket as a meter. In the second version, the traffic passes through a queue that is the analogue of the bucket, i.e. the traffic is the analogue of the water passing through the bucket. This version is referred to here as the leaky bucket as a queue. The leaky bucket as a meter is equivalent to (a mirror image of) the token bucket
Token bucket
The token bucket is an algorithm used in packet switched computer networks and telecommunications networks to check that data transmissions conform to defined limits on bandwidth and burstiness ....
algorithm, and given the same parameters will see the same traffic as conforming or nonconforming. The leaky bucket as a queue can be seen as a special case of the leaky bucket as a meter.
A version of the leaky bucket algorithm, the Generic Cell Rate Algorithm
Generic cell rate algorithm
The Generic Cell Rate Algorithm is an algorithm that is used in Asynchronous Transfer Mode networks to measure the timing of cells on Virtual Channels and or Virtual Paths against bandwidth and jitter limits contained in a traffic contract for the VC or VP to which the cells belong...
, is recommended for Asynchronous Transfer Mode
Asynchronous Transfer Mode
Asynchronous Transfer Mode is a standard switching technique designed to unify telecommunication and computer networks. It uses asynchronous time-division multiplexing, and it encodes data into small, fixed-sized cells. This differs from approaches such as the Internet Protocol or Ethernet that...
networks in Usage/Network Parameter Control at User–Network Interfaces or Inter-Network Interfaces or Network-Network Interfaces
NNI
In telecommunications, a network-to-network Interface is an interface which specifies signaling and management functions between two networks. NNI circuit can be used for interconnection of either signalling , IP In telecommunications, a network-to-network Interface (NNI) is an interface which...
. The Generic Cell Rate Algorithm, or an equivalent, may also be used to control transmissions by a Network Interface Card onto an ATM network (i.e. on the user side of the User-Network Interface).
The Leaky Bucket Algorithm as a Meter
Jonathan S. TurnerJonathan S. Turner
Jonathan Turner is the Barbara J. and Jerome R. Cox, Jr. Professor of Computer Science at Washington University in St. Louis. His research interests include the design and analysis of high performance routers and switching systems, extensible communication networks and analysis of algorithms.In...
is credited with the original description of the leaky bucket algorithm and describes it as follows: “A counter associated with each user transmitting on a connection is incremented whenever the user sends a packet and is decremented periodically. If the counter exceeds a threshold upon being incremented, the network discards the packet. The user specifies the rate at which the counter is decremented (this determines the average bandwidth) and the value of the threshold (a measure of burstiness)”. The bucket (analogous to the counter) is in this case used as a meter to test the conformance of packets, rather than as a queue to directly control them.
Another version of what is essentially the same meter version of the algorithm, the Generic Cell Rate Algorithm
Generic cell rate algorithm
The Generic Cell Rate Algorithm is an algorithm that is used in Asynchronous Transfer Mode networks to measure the timing of cells on Virtual Channels and or Virtual Paths against bandwidth and jitter limits contained in a traffic contract for the VC or VP to which the cells belong...
, is described by the ITU-T
ITU-T
The ITU Telecommunication Standardization Sector is one of the three sectors of the International Telecommunication Union ; it coordinates standards for telecommunications....
in recommendation I.371. and in the ATM Forum
ATM Forum
The ATM Forum was founded in 1991 to be the industry consortium to promote Asynchronous Transfer Mode technology used in telecommunication networks. It was a non-profit international organization. The ATM Forum created over 200 implementation agreements....
’s UNI Specification. The description, in which the term cell is equivalent to packet in Turner's description is given by the ITU-T as follows: “The continuous-state leaky bucket can be viewed as a finite capacity bucket whose real-valued content drains out at a continuous rate of 1 unit of content per time unit and whose content is increased by the increment T for each conforming cell... If at a cell arrival the content of the bucket is less than or equal to the limit value τ, then the cell is conforming; otherwise, the cell is non-conforming. The capacity of the bucket (the upper bound of the counter) is (T + τ)”.
David E. McDysan and Darrel L. Spohn provide a commentary on the description given by the ITU-T/ATM Forum. In this they state “In the leaky bucket analogy, the [ATM] cells do not actually flow through the bucket; only the check for conforming admission does”. However, uncommonly in the descriptions in the literature, McDysan and Spohn also refer to the leaky bucket algorithm as a queue, going on “Note that one implementation of traffic shaping is to actually have the cells flow through the bucket”.
In describing the operation of the ITU-T's version of the algorithm, McDysan and Spohn invoke a “notion commonly employed in queueing theory
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
of a fictional ‘gremlin’”. This gremlin inspects the level in the bucket and takes action if the level is above the limit value τ : in policing (figure 2), it pulls open a trap door, which causes the packet to be dropped and stops its water from entering the bucket; in shaping (figure 3), it pushes up a flap, which delays the packet and prevents it from delivering its water, until the water level in the bucket falls below τ.
The difference between the descriptions given by Turner and the ITU-T/ATM Forum is that Turner's is specific to traffic policing, whereas the ITU-T/ATM Forum's is applicable to both traffic policing and traffic shaping. Also, Turner does not state that the contents of the counter should only be affected by conforming packets, and should only be incremented when this would not cause it to exceed the threshold, i.e. Turner does not explicitly state that the bucket’s capacity or counter's maximum value is finite. To make Turner’s description clearly aligned with ITU-T, the statement “If the counter exceeds a threshold upon being incremented, the network discards the packet” would have to be changed to something like “If the counter would exceed a threshold upon being incremented, the network discards the packet and the counter is not incremented”.
In fairness, the description given by Turner is in terms of a traffic policing function, where overzealousness in limiting a connection containing nonconforming packets may not be an issue. Indeed, in some contexts, such as Variable bitrate
Variable bitrate
Variable bitrate is a term used in telecommunications and computing that relates to the bitrate used in sound or video encoding. As opposed to constant bitrate , VBR files vary the amount of output data per time segment...
(VBR) transmissions, the loss of any one packet may corrupt the entirety of a higher layer message, e.g. an OSI Network Layer PDU. In which case, discarding all the following packets of that corrupted PDU sheds an unnecessary network load. However, it would be entirely unacceptable in traffic shaping for a packet that fails the conformance test to affect how long before conformance can next occur, i.e. if the act of testing would change how long the packet has to wait.
Neither Turner nor the ITU-T addresses the issue of variable length packets. To be fair again, the description according to the ITU-T is for ATM cells, which are fixed length packets, and Turner does not specifically exclude variable length packets. In both cases, if the amount by which the bucket content or counter is incremented for a conforming packet is proportional to the packet length, they will both account for the length and allow the algorithm to limit the bandwidth of the traffic explicitly rather than limiting the packet rate.
Concept of Operation
A description of the concept of operation of the Leaky Bucket Algorithm as a meter that can be used in either traffic policing or traffic shaping, may be stated as follows:- A fixed capacity bucket, associated with each virtual connection or user, leaks at a fixed rate.
- If the bucket is empty, it stops leaking.
- For a packet to conform, it has to be possible to add a specific amount of water to the bucket: The specific amount added by a conforming packet can be the same for all packets, or can be proportional to the length of the packet.
- If this amount of water would cause the bucket to exceed its capacity then the packet does not conform and the water in the bucket is left unchanged.
Uses
The leaky bucket as a meter can be used in either traffic shapingTraffic shaping
Traffic shaping is the control of computer network traffic in order to optimize or guarantee performance, improve latency, and/or increase usable bandwidth for some kinds of packets by delaying other kinds of packets that meet certain criteria...
or traffic policing
Traffic policing
Traffic policing is the process of monitoring network traffic for compliance with a traffic contract and taking steps to enforce that contract. Traffic sources which are aware of a traffic contract may apply traffic shaping to ensure their output stays within the contract and is thus not discarded...
. For example, in ATM networks, in the form of the Generic Cell Rate Algorithm, it is used to compare the bandwidth and burstiness of traffic on a Virtual Channel or Virtual Path against the specified limits. In traffic policing, nonconforming cells may be discarded (dropped) or may be reduced in priority (for downstream traffic management functions to drop if there is congestion). In traffic shaping, cells are delayed until they conform. Traffic policing and traffic shaping are commonly used in UPC/NPC to protect the network against excess or excessively bursty traffic, see bandwidth management
Bandwidth management
Bandwidth management is the process of measuring and controlling the communications on a network link, to avoid filling the link to capacity or overfilling the link, which would result in network congestion and poor performance of the network.- Management :Bandwidth management mechanisms may be...
and congestion avoidance. Traffic shaping is commonly used in the network interfaces in hosts to prevent transmissions being discarded by traffic management functions in the network.
The leaky bucket algorithm as a meter can also be used in a leaky bucket counter to measure the rate of random or stochastic processes. A Leaky bucket counter can be used to detect when the average or peak rate of events increases above some, acceptable, background level, i.e. when the bucket overflows. However, events that do not cause an overflow, i.e. have sufficiently low rates and are well distributed over time, can be ignored. For example, such a leaky bucket counter can be used to detect when there is a sudden burst of correctable memory errors or when there has been a gradual, but significant, increase in the average rate, which may indicate an impending failure, etc.
The use of the leaky bucket algorithm in a leaky bucket counter is similar to that in traffic management, in that it is used as a meter. Essentially, the events replace the packets in the description, with each event causing a quantity of water to be added to the bucket. If the bucket would overflow, as a result of the event, then the event should trigger the action associated with an out of limits event. Some implementations seem to parallel Turner's description, in that there is no explicit limit on the maximum value that the counter may take, implying that once the counter has exceeded the threshold, it may not return to its previous state until a period significantly greater than the equivalent of the emission interval has passed, which may be increased by what would otherwise be conforming events. Other implementations may, however, not increment the counter while it is overflowed, allowing it to correctly determine whether following events conform or not.
Parameters
In the case of the leaky bucket algorithm as a meter, the limits on the traffic can be a bandwidth and a burstiness of the output.The bandwidth limit and burstiness limit for the connection may be specified in a traffic contract
Traffic contract
If a service wishes to use a broadband network to transport a particular kind of traffic, it must first inform the network about what kind of traffic is to be transported, and the performance requirements of that traffic...
. A bandwidth limit may be specified as a packet or frame rate, a byte or bit rate
Bit rate
In telecommunications and computing, bit rate is the number of bits that are conveyed or processed per unit of time....
, or as an emission interval between the packets. A limit on burstiness may be specified as a jitter
Jitter
Jitter is the undesired deviation from true periodicity of an assumed periodic signal in electronics and telecommunications, often in relation to a reference clock source. Jitter may be observed in characteristics such as the frequency of successive pulses, the signal amplitude, or phase of...
or delay variation tolerance, or as a maximum burst size (MBS).
Multiple sets of contract parameters can be applied concurrently to a connection using multiple instances of the leaky bucket algorithm, each of which may take a bandwidth and a burstiness limit: see Dual Leaky Bucket Controller.
Emission Interval
The rate at which the bucket leaks determines the bandwidth limit, which is referred to as the average rate by Turner and the inverse of which is referred to as the emission interval by the ITU-T. It is easiest to explain what this interval is where packets have a fixed length. Hence, the first part of this description assumes this, and the implications of variable packet lengths are considered separately.Consider a bucket that is exactly filled to the top by preceding traffic, i.e. when the maximum permitted burstiness has already occurred. The minimum interval before the next packet can conform is then the time it takes for the bucket to leak exactly the amount of water delivered by a packet, and if a packet is tested and conforms at that time, this will exactly fill the bucket once more. Thus, once the bucket is filled, the maximum rate that packets can conform is with this interval between each packet.
Turner refers to this rate as the average, implying that its inverse is the average interval. There is, however, some ambiguity in what the average rate and interval are. Since, packets can arrive at any lower rate, this is an upper bound, rather than a fixed value, so it could at best be called the maximum for the average rate. Also, during the time the maximum burstiness occurs, packets can arrive with smaller intervals and thus a higher rate than this. So, for any period less than infinity, the actual average rate can be (but isn’t necessarily) greater than this and the average interval can be (but isn’t necessarily) less than the emission interval. Hence, because of this ambiguity, the term emission interval is used hereafter. However, it is still true that the minimum value that the long term average interval can take tends to be the emission interval.
For variable length packets, where the amount added to the bucket is proportional to the packet length, the maximum rate at which they can conform varies according to their length: the amount that the bucket must have leaked from full for a packet to conform is the amount the packet will add, and if this is proportional to the packet length, so is the interval between it and the preceding packet that filled the bucket. Hence, it is not possible to specify a specific emission interval for variable length packets, and the bandwidth limit has to be specified explicitly, in bits or bytes per second.
Delay Variation Tolerance
It is easiest to explain what this tolerance is where packets have a fixed length. Hence, the first part of this description assumes this, and the implications of variable packet lengths are considered separately.The ITU-T define a limit value, τ that is T less than the capacity of the bucket. This limit values specifies how much earlier a packet can arrive than it would normally be expected if the packets were arriving with exactly the emission interval between them.
Imagine the following situation: A bucket leaks at 1 unit of water per second, so the limit value, τ and the amount of water added by a packet, T, are effectively in units of seconds. This bucket starts off empty, so the first packet to arrive must conform. The bucket then becomes exactly full after a number of conforming packets, N, have arrived in the minimum possible time to conform. For the last (Nth) packet to conform, the bucket must have leaked enough of the water from the preceding N – 1 packets ((N – 1) * T seconds worth) for it to be exactly at the limit value τ at this time. Hence, the water leaked is (N– 1)T – τ, which because the leak is one unit per second, took exactly (N– 1)T – τ seconds to leak. Thus the shortest time in which all N packets can arrive and conform is (N– 1)T – τ seconds, which is exactly τ less than the time it would have taken if the packets had been arriving at exactly the emission interval.
Since the limit value τ defines how much earlier a packet can arrive than would be expected, it is the limit on the difference between the maximum and minimum delays from the source (assuming the packets are generated with no jitter) to the point where the conformance test is being made. Hence, the use of the term Cell Delay Variation tolerance (CDVt) for this parameter in ATM.
As an example, a possible source of delay variation is where a number of connections (streams of packets) are multiplexed together at the output of a switch. Assuming that the sum of the bandwidths of these connections is less than that of the output, all of the packets that arrive can be transmitted, eventually. However, if their arrivals are independent, e.g. because they arrive at different inputs of the switch, then several may arrive at or nearly at the same time. Since the output can only transmit one packet at a time, the others must be queued in a buffer until it is their turn to be transmitted. This buffer then introduces an additional delay between a packet arriving at an input and being transmitted by the output, and this delay varies, depending on how many other packets are already queued in the buffer. A similar situation can occur at the output of a host (in the NIC) when multiple packets have the same or similar release times, and this delay can usually be modelled as a delay in a virtual output buffer.
For variable length packets, where the amount of water added by a given packet is proportional to its length, τ can’t be seen as a limit on how full the bucket can be, as this varies depending on the packet size. However, the time it takes to drain from this level to empty is still how much earlier a packet can arrive than is expected, when packets are transmitted at the bandwidth limit. Thus, it is still the maximum variation in transfer delay to the point where the conformance test is being applied that can be tolerated, and thus the tolerance on maximum delay variation.
Maximum Burst Size
The limit value or delay variation tolerance also controls how many packets can arrive back-to-back at the physical layer line rate, i.e. in a burst. Hence it is possible to specify the burstiness limit as an MBS and derive the limit value τ from this or to specify it as a jitter/delay variation tolerance, and derive the MBS from this.If the limit value is large enough, then several packets can arrive back-to-back and still conform: if the bucket starts from empty, the first packet to arrive will add T, but if, by the time the next packet arrives, the contents is below τ, this will also conform. Assuming that each packet takes δ to arrive at the line rate, then if τ (expressed as the time it takes the bucket to empty from the limit value) is equal to or greater than 'the emission interval less the minimum interarrival time, T – δ, the second packet will conform even if it arrives back-to-back with the first. Similarly, if τ is equal to or greater than (T – δ) × 2, then 3 packets can arrive back-to-back, etc.
The maximum size of this burst, M, can be calculated from the emission interval, T; the maximum jitter tolerance, τ; and the time taken to transmit/receive a packet, δ, as follows:
Equally, the minimum value of jitter tolerance τ that gives a specific MBS can be calculated from the MBS as follows:
For variable length packets, the maximum burst size will depend on the lengths of the packets in the burst and there is no single value for the maximum burst size. However, it is possible to specify the total burst length in bytes, from the byte rate of the input stream, the equivalent byte rate of the leak, and the bucket depth.
Comparison with the Token Bucket Algorithm
The leaky bucket algorithm is sometimes contrasted with the token bucketToken bucket
The token bucket is an algorithm used in packet switched computer networks and telecommunications networks to check that data transmissions conform to defined limits on bandwidth and burstiness ....
algorithm. However, the above concept of operation for the leaky bucket as a meter may be directly compared with the token bucket algorithm
Token bucket
The token bucket is an algorithm used in packet switched computer networks and telecommunications networks to check that data transmissions conform to defined limits on bandwidth and burstiness ....
, the description of which is given in that article as the following:
- A token is added to the bucket every 1/r seconds.
- The bucket can hold at the most b tokens. If a token arrives when the bucket is full, it is discarded.
- When a packet (network layer PDUProtocol data unitIn telecommunications, the term protocol data unit has the following meanings:#Information that is delivered as a unit among peer entities of a network and that may contain control information, address information, or data....
) [sic] of "n" bytes arrives, n tokens are removed from the bucket, and the packet is sent to the network.
- If fewer than n tokens are available, no tokens are removed from the bucket, and the packet is considered to be non-conformant.
This can be compared with the concept of operation, repeated from above:
- A fixed capacity bucket, associated with each virtual connection or user, leaks at a fixed rate.
- If the bucket is empty, it stops leaking.
- For a packet to conform, it has to be possible to add a specific amount of water to the bucket: The specific amount added by a conforming packet can be the same for all packets, or can be proportional to the length of the packet.
- If this amount of water would cause the bucket to exceed its capacity then the packet does not conform and the water in the bucket is left unchanged.
As can be seen, these two descriptions are essentially mirror images of one another: one adds something to the bucket on a regular basis and takes something away for conforming packets down to a limit of zero; the other takes away regularly and adds for conforming packets up to a limit of the bucket's capacity. It would also be perfectly possible to describe the process in terms of adding tokens or subtracting water for conforming packets as long as the regular process complements this, at which point it would become impossible to tell which was which: is an implementation that removes tokens regularly and adds tokens for a conforming packet an implementation of the leaky bucket or of the token bucket? In fact it is both, as these are the same basic algorithm described differently. This explains why, given equivalent parameters, the two algorithms will see exactly the same packets as conforming or nonconforming.
The differences in the properties and performance of implementations of the leaky and token bucket algorithms thus result entirely form the differences in the implementations, i.e. they do not stem from differences in the underling algorithms.
The points to note are that the leaky bucket algorithm, when used as a meter, can allow a conforming output packet stream with jitter or burstiness, can be used in traffic policing as well as shaping, and can be implemented for variable length packets.
The Leaky Bucket Algorithm as a Queue
A seminal description of the leaky bucket as a queue is given by Andrew S. TanenbaumAndrew S. Tanenbaum
Andrew Stuart "Andy" Tanenbaum is a professor of computer science at the Vrije Universiteit, Amsterdam in the Netherlands. He is best known as the author of MINIX, a free Unix-like operating system for teaching purposes, and for his computer science textbooks, regarded as standard texts in the...
, in his book Computer Networks as “The leaky bucket consists of a finite queue. When a packet arrives, if there is room on the queue it is appended to the queue; otherwise it is discarded. At every clock tick one packet is transmitted (unless the queue is empty)”.
As can be seen this implementation is restricted in that the packets are only ever transmitted at a fixed rate. To underline this, Tanenbaum also states that “The leaky bucket algorithm enforces a rigid output pattern at the average rate, no matter how bursty the [input] traffic is”. An implementation of the leaky bucket as a queue is therefore always a form of traffic shaping function.
A further restriction is that the leaky bucket as a queue traffic shaping function only transmits packets on the ticks; hence, if it is used within a network, equivalent to UPC and NPC, it also imposes a fixed phase on the onward transmission of packets. Perversely, in the context of the transfer delay, this imposition of a fixed phase that may be different from that of an otherwise conforming input packet stream, constitutes a delay variation and hence a jitter.
Limiting variable length packets using the leaky bucket algorithm as a queue is significantly more complicated than it is for fixed length packets. Tanenbaum gives a description of a “byte-counting” leaky bucket for variable length packets as follows: “At each tick, a counter is initialized to n. If the first packet on the queue has fewer bytes than the current value of the counter, it is transmitted, and the counter is decremented by that number of bytes. Additional packets may also be sent, as long as the counter is high enough. When the counter drops below the length of the next packet on the queue, transmission stops until the next tick, at which time the residual byte count is reset [to n] and the flow can continue”.
Uses
The leaky bucket as a queue can only be used in shapingTraffic shaping
Traffic shaping is the control of computer network traffic in order to optimize or guarantee performance, improve latency, and/or increase usable bandwidth for some kinds of packets by delaying other kinds of packets that meet certain criteria...
traffic to a specified bandwidth with no jitter in the output. It may be used within the network, e.g. as part of bandwidth management, etc., but is more appropriate to traffic shaping in the network interfaces of hosts.
Parameters
In the case of the leaky bucket algorithm as a queue, the only defined limit for this algorithm is the bandwidth of its output.The bandwidth limit for the connection may be specified in a traffic contract
Traffic contract
If a service wishes to use a broadband network to transport a particular kind of traffic, it must first inform the network about what kind of traffic is to be transported, and the performance requirements of that traffic...
. A bandwidth limit may be specified as a packet or frame rate, a byte or bit rate
Bit rate
In telecommunications and computing, bit rate is the number of bits that are conveyed or processed per unit of time....
, or as an emission interval between the packets.
Inefficiency of the leaky-bucket as a queue implementation
The implementation of the leaky-bucket as a queue does not use available network resources efficiently. Because it transmits packets only at fixed intervals, there will be many instances when the traffic volume is very low and large portions of network resources (bandwidth in particular) are not being used. Therefore no mechanism exists in the leaky-bucket implementation as a queue to allow individual flows to burst up to port speed, effectively consuming network resources at times when there would not be resource contention in the network. Implementations of the token bucket and leaky bucket as a meter do, however, allow output traffic flows to have bursty characteristics.Comparison Between the two Versions of the Leaky Bucket Algorithm
Analysis of the two versions of the leaky bucket algorithm shows that the version as a queue is a special case of the version as a meter.Imagine a traffic shaping function for fixed length packets that is implemented using a fixed length queue, forming a delay element, which is serviced using a leaky bucket as a meter. Imagine also that the bucket in this meter has a depth equal to the amount added by a packet, i.e. has a limit value, τ, of zero. However, the conformance test is only performed at intervals of the emission interval, when the packet at the head of the queue is transmitted and its water is added. This water then leaks away during the next emission interval, allowing the next packet to conform then or at some subsequent emission interval. The service function can also be viewed in terms of a token bucket with the same depth, where enough tokens for one packet are added over the emission interval. This implementation will then receive packets with a bursty arrival pattern (limited by the queue depth) and transmit them on at intervals that are always exact (integral) multiples of the emission interval.
However, the implementation of the leaky bucket as a meter (or token bucket) in a traffic shaping function described above is an exact equivalent to the description of the leaky bucket as a queue: the delay element of the meter version is the bucket of the queue version; the bucket of the meter version is the process that services the queue, and the leak is such that the emission interval is the same as the tick interval. Therefore for fixed length packets, the implementation of the leaky bucket as a queue is of a special case of a traffic shaping function using a leaky bucket (or token bucket) as a meter in which the limit value, τ, is zero and the process is performed at the lowest possible rate.
The leaky bucket as a queue for variable packet lengths can also be described as equivalent to a special case of the leaky bucket as a meter. The suggested implementation can, like the fixed length implementation, be seen as traffic shaping function in which the queue is a delay element, rather than the bucket, and the function that services the queue is, in this case, explicitly given as a token bucket: it is decremented for conforming packets and incremented at a fixed rate. Hence, as the leaky bucket as a meter and token bucket are equivalent, the leaky bucket as a queue for variable packet lengths is also a special case of a traffic shaping function using a leaky bucket (or token bucket) as a meter.
There is an interesting consequence of seeing the leaky bucket as a queue for variable packet lengths as a specific implementation of the token bucket or leaky bucket as a meter in traffic shaping. This is that the bucket of the meter has a depth, n, and, as is always the case with the token bucket, this depth determines the burstiness of the output traffic (perhaps in relation to the average or minimum number of tokens required by the packets). Hence, it is possible to quantify the burstiness of the output of this "byte counting" leaky bucket as a meter, unless all packets are of the maximum length when it becomes pointless. However, this ability to define a burstiness for the output is in direct contradiction to the statement that the leaky bucket (as a queue) necessarily gives an output with a rigid rate, no matter how bursty the input.
See also
- Generic Cell Rate AlgorithmGeneric cell rate algorithmThe Generic Cell Rate Algorithm is an algorithm that is used in Asynchronous Transfer Mode networks to measure the timing of cells on Virtual Channels and or Virtual Paths against bandwidth and jitter limits contained in a traffic contract for the VC or VP to which the cells belong...
- UPC and NPC
- Traffic contractTraffic contractIf a service wishes to use a broadband network to transport a particular kind of traffic, it must first inform the network about what kind of traffic is to be transported, and the performance requirements of that traffic...
- Connection admission control
- Traffic shapingTraffic shapingTraffic shaping is the control of computer network traffic in order to optimize or guarantee performance, improve latency, and/or increase usable bandwidth for some kinds of packets by delaying other kinds of packets that meet certain criteria...
- Traffic policingTraffic policingTraffic policing is the process of monitoring network traffic for compliance with a traffic contract and taking steps to enforce that contract. Traffic sources which are aware of a traffic contract may apply traffic shaping to ensure their output stays within the contract and is thus not discarded...
- Token bucketToken bucketThe token bucket is an algorithm used in packet switched computer networks and telecommunications networks to check that data transmissions conform to defined limits on bandwidth and burstiness ....