
Leapfrog integration
Encyclopedia
Leapfrog integration is a simple method for numerically integrating differential equation
s of the form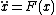 ,
,
or equivalently of the form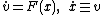 ,
,
particularly in the case of a dynamical system
of classical mechanics. Such problems often take the form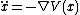 ,
,
with energy function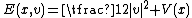 ,
,
where V is the potential energy of the system. The method is known by different names in different disciplines. In particular, it is similar to the Velocity Verlet method, which is a variant of Verlet integration
. Leapfrog integration is equivalent to updating positions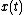 and velocities
and velocities 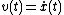 at interleaved time points, staggered in such a way that they 'leapfrog' over each other. For example, the position is updated at integer time steps and the velocity is updated at integer-plus-a-half time steps.
at interleaved time points, staggered in such a way that they 'leapfrog' over each other. For example, the position is updated at integer time steps and the velocity is updated at integer-plus-a-half time steps.
Leapfrog integration is a second order method, in contrast to Euler integration
, which is only first order, yet requires the same number of function evaluations per step. Unlike Euler integration, it is stable for oscillatory motion, as long as the time-step, .
.
In leapfrog integration, the equations for updating position and velocity are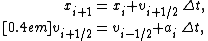
where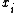 is position at step
is position at step 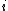 ,
, 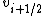 is the velocity, or first derivative of
is the velocity, or first derivative of  , at step
, at step 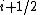 ,
, 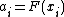 is the acceleration, or second derivative of
is the acceleration, or second derivative of  , at step
, at step 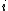 and
and  is the size of each time step. These equations can be expressed in a form which gives velocity at integer steps as
is the size of each time step. These equations can be expressed in a form which gives velocity at integer steps as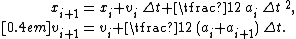
One use of this equation is in gravity simulations, since in that case the acceleration depends only on the positions of the gravitating masses, although higher order integrators (such as Runge–Kutta methods
) are more frequently used.
There are two primary strengths to Leapfrog integration when applied to mechanics problems. The first is the time-reversibility of the Leapfrog method. One can integrate forward n steps, and then reverse the direction of integration and integrate backwards n steps to arrive at the same starting position. The second strength of Leapfrog integration is its symplectic
nature, which implies that it conserves the (slightly modified) energy of dynamical systems. This is especially useful when computing orbital dynamics, as other integration schemes, such as the Runge-Kutta method, do not conserve energy and allow the system to drift substantially over time.
Because of its time-reversibility, and because it is a symplectic integrator
, leapfrog integration is also used in Hamiltonian Monte Carlo
, a method for drawing random samples from a probability distribution whose overall normalization is unknown.
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s of the form
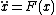 ,
,or equivalently of the form
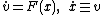 ,
,particularly in the case of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
of classical mechanics. Such problems often take the form
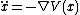 ,
,with energy function
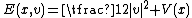 ,
,where V is the potential energy of the system. The method is known by different names in different disciplines. In particular, it is similar to the Velocity Verlet method, which is a variant of Verlet integration
Verlet integration
Verlet integration is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics...
. Leapfrog integration is equivalent to updating positions
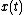 and velocities
and velocities 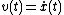 at interleaved time points, staggered in such a way that they 'leapfrog' over each other. For example, the position is updated at integer time steps and the velocity is updated at integer-plus-a-half time steps.
at interleaved time points, staggered in such a way that they 'leapfrog' over each other. For example, the position is updated at integer time steps and the velocity is updated at integer-plus-a-half time steps.Leapfrog integration is a second order method, in contrast to Euler integration
Euler integration
In mathematics and computational science, the Euler method, named after Leonhard Euler, is a first-order numerical procedure for solving ordinary differential equations with a given initial value...
, which is only first order, yet requires the same number of function evaluations per step. Unlike Euler integration, it is stable for oscillatory motion, as long as the time-step,
 .
.In leapfrog integration, the equations for updating position and velocity are
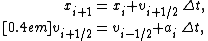
where
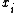 is position at step
is position at step 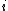 ,
, 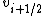 is the velocity, or first derivative of
is the velocity, or first derivative of  , at step
, at step 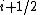 ,
, 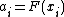 is the acceleration, or second derivative of
is the acceleration, or second derivative of  , at step
, at step 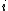 and
and  is the size of each time step. These equations can be expressed in a form which gives velocity at integer steps as
is the size of each time step. These equations can be expressed in a form which gives velocity at integer steps as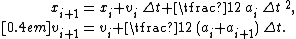
One use of this equation is in gravity simulations, since in that case the acceleration depends only on the positions of the gravitating masses, although higher order integrators (such as Runge–Kutta methods
Runge–Kutta methods
In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...
) are more frequently used.
There are two primary strengths to Leapfrog integration when applied to mechanics problems. The first is the time-reversibility of the Leapfrog method. One can integrate forward n steps, and then reverse the direction of integration and integrate backwards n steps to arrive at the same starting position. The second strength of Leapfrog integration is its symplectic
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
nature, which implies that it conserves the (slightly modified) energy of dynamical systems. This is especially useful when computing orbital dynamics, as other integration schemes, such as the Runge-Kutta method, do not conserve energy and allow the system to drift substantially over time.
Because of its time-reversibility, and because it is a symplectic integrator
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
, leapfrog integration is also used in Hamiltonian Monte Carlo
Hybrid Monte Carlo
In mathematics and physics, the Hybrid Monte Carlo algorithm, also known as Hamiltonian Monte Carlo, is a Markov chain Monte Carlo method for obtaining a sequence of random samples from a probability distribution for which direct sampling is difficult...
, a method for drawing random samples from a probability distribution whose overall normalization is unknown.
See also
- Numerical ordinary differential equationsNumerical ordinary differential equationsNumerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
- Euler integrationEuler integrationIn mathematics and computational science, the Euler method, named after Leonhard Euler, is a first-order numerical procedure for solving ordinary differential equations with a given initial value...
- Verlet integrationVerlet integrationVerlet integration is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics...
- Runge–Kutta integrationRunge–Kutta methodsIn numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...

