
Lee–Yang theorem
Encyclopedia
In statistical mechanics
, the Lee–Yang theorem states that if partition functions
of certain models in statistical field theory
with ferromagnetic interactions are considered as functions of an external field, then all zeros
are purely imaginary (or on the unit circle after a change of variable). The first version was proved for the Ising model
by . Their result was later extended to more general models by several people.
extended the Lee–Yang theorem to certain continuous probability distributions by approximating them by a superposition of Ising models. gave a general theorem stating roughly that the Lee–Yang theorem holds for a ferromagnetic interaction provided it holds for zero interaction. generalized Newman
's result from measures on R to measures on higher-dimensional Euclidean space.
There has been some speculation about a relationship between the Lee–Yang theorem and the Riemann hypothesis
about the Riemann zeta function; see .
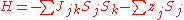
and is said to be ferromagnetic if all the numbers Jjk are non-negative reals.
The partition function
is given by
where each dμj is an even measure on the reals R decreasing at infinity so fast that
all Gaussian functions are integrable.
A rapidly decreasing measure on the reals is said to have the Lee-Yang property if all zeros of its Fourier transform are real.
the partition function is non-zero. In particular if all the numbers zj are equal to some number z, then all zeros of the partition function (considered as a function of z) are imaginary.
In the original Ising model case considered by Lee and Yang, the measures all have support on the 2 point set −1, 1,
so the partition function can be considered a function of the variable ρ = eπz. With this change of variable the Lee–Yang theorem says that all zeros ρ lie on the unit circle.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Lee–Yang theorem states that if partition functions
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of certain models in statistical field theory
Statistical field theory
A statistical field theory is any model in statistical mechanics where the degrees of freedom comprise a field or fields. In other words, the microstates of the system are expressed through field configurations...
with ferromagnetic interactions are considered as functions of an external field, then all zeros
are purely imaginary (or on the unit circle after a change of variable). The first version was proved for the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
by . Their result was later extended to more general models by several people.
extended the Lee–Yang theorem to certain continuous probability distributions by approximating them by a superposition of Ising models. gave a general theorem stating roughly that the Lee–Yang theorem holds for a ferromagnetic interaction provided it holds for zero interaction. generalized Newman
Charles M. Newman
Charles Michael "Chuck" Newman is a mathematician and a physicist at the Courant Institute of Mathematical Sciences of New York University...
's result from measures on R to measures on higher-dimensional Euclidean space.
There has been some speculation about a relationship between the Lee–Yang theorem and the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
about the Riemann zeta function; see .
Preliminaries
The Hamiltonian is given by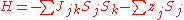
and is said to be ferromagnetic if all the numbers Jjk are non-negative reals.
The partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is given by

where each dμj is an even measure on the reals R decreasing at infinity so fast that
all Gaussian functions are integrable.
A rapidly decreasing measure on the reals is said to have the Lee-Yang property if all zeros of its Fourier transform are real.
Theorem
The Lee–Yang theorem states that if the Hamiltonian is ferromagnetic and all the measures dμj have the Lee-Yang property, and all the numbers zj have positive real part, thenthe partition function is non-zero. In particular if all the numbers zj are equal to some number z, then all zeros of the partition function (considered as a function of z) are imaginary.
In the original Ising model case considered by Lee and Yang, the measures all have support on the 2 point set −1, 1,
so the partition function can be considered a function of the variable ρ = eπz. With this change of variable the Lee–Yang theorem says that all zeros ρ lie on the unit circle.
Examples
Some examples of measure with the Lee-Yang property are:- The measure of the Ising model, which has support consisting of two points (usually 1 and −1) each with weight 1/2. This is the original case considered by Lee and Yang.
- The distribution of spin n/2, whose support has n+1 equally spaced points, each of weight 1/(n + 1). This is a generalization of the Ising model case.
- The density of measure uniformly distributed between −1 and 1.
- The density
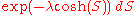
- The density
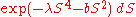 for positive λ and real b. This corresponds to the (φ4)2 Euclidean quantum field theory.
for positive λ and real b. This corresponds to the (φ4)2 Euclidean quantum field theory. - The density
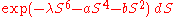 for positive λ does not always have the Lee-Yang property.
for positive λ does not always have the Lee-Yang property. - If dμ has the Lee-Yang property, so does exp(bS2) dμ for any positive b.
- If dμ has the Lee-Yang property, so does Q(S) dμ for any even polynomial Q all of whose zeros are imaginary.
- The convolution of two measures with the Lee-Yang property also has the Lee-Yang property.

