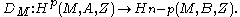In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Lefschetz duality is a version of Poincaré duality

Poincaré duality

In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...

 in geometric topology

Geometric topology

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...

, applying to a manifold with boundary. Such a formulation was introduced by Solomon Lefschetz

Solomon Lefschetz

Solomon Lefschetz was an American mathematician who did fundamental work on algebraic topology, its applications to algebraic geometry, and the theory of non-linear ordinary differential equations.-Life:...

 in the 1920s, at the same time introducing relative homology

Relative homology

In algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...

, for application to the Lefschetz fixed-point theorem

Lefschetz fixed-point theorem

In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X...

. There are now numerous formulations of Lefschetz duality or Poincaré-Lefschetz duality, or Alexander-Lefschetz duality.

Formulations

Let M be an orientable compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

 manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 of dimension n, with boundary N, and let z be the fundamental class

Fundamental class

In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...

 of M. Then cap product

Cap product

In algebraic topology the cap product is a method of adjoining a chain of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech in 1936, and independently by Hassler Whitney in 1938.-Definition:Let X be a topological...

 with z induces a pairing of the (co)homology groups of M and the relative (co)homology of the pair (M, N); and this gives rise to isomorphisms of H^k(M, N) with H_{n - k}(M), and of H_k(M, N) with H^{n - k}(M).

Here N can in fact be empty, so Poincaré duality appears as a special case of Lefschetz duality.

There is a version for triples. Let A and B denote two subspaces of the boundary N, themselves compact orientable manifolds with common boundary Z, which is the intersection of A and B. Then there is an isomorphism