Lefschetz zeta function
Encyclopedia
In mathematics
, the Lefschetz zeta-function is a tool used in topological periodic and fixed point
theory, and dynamical systems. Given a mapping ƒ, the zeta-function is defined as the formal series
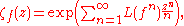
where L(ƒ n) is the Lefschetz number of the nth iterate
of ƒ. This zeta-function is of note in topological periodic point theory because it is a single invariant containing information about all iterates of ƒ.
where χ(X) is the Euler characteristic
of X, i.e., the Lefschetz number of the identity map.
For a less trivial example, consider as space the unit circle
, and let ƒ be its reflection in the x-axis, or in other words θ → −θ. Then ƒ has Lefschetz number 2, and ƒ2 is the identity map, which has Lefschetz number 0. All odd iterates have Lefschetz number 2, all even iterates have Lefschetz number 0. Therefore the zeta function of ƒ is
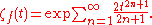
Via intermediate expressions
This is seen to be equal to
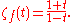
is a continuous map on a compact manifold 
of dimension 
(or more generally any compact polyhedron), the zeta function is given by the formula
Thus it is a rational function. The polynomials occurring in the numerator and denominator are essentially the characteristic polynomials of the map induced by
on the various homology spaces.
ic form of the Artin–Mazur zeta-function, which gives geometric
information about the fixed and periodic points of ƒ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lefschetz zeta-function is a tool used in topological periodic and fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
theory, and dynamical systems. Given a mapping ƒ, the zeta-function is defined as the formal series
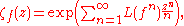
where L(ƒ n) is the Lefschetz number of the nth iterate
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of ƒ. This zeta-function is of note in topological periodic point theory because it is a single invariant containing information about all iterates of ƒ.
Examples
The identity map on X has Lefschetz zeta function- 1/(1 − t)χ(X),
where χ(X) is the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of X, i.e., the Lefschetz number of the identity map.
For a less trivial example, consider as space the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, and let ƒ be its reflection in the x-axis, or in other words θ → −θ. Then ƒ has Lefschetz number 2, and ƒ2 is the identity map, which has Lefschetz number 0. All odd iterates have Lefschetz number 2, all even iterates have Lefschetz number 0. Therefore the zeta function of ƒ is
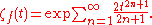
Via intermediate expressions
This is seen to be equal to
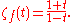
Formula
If is a continuous map on a compact manifold of dimension (or more generally any compact polyhedron), the zeta function is given by the formulaThus it is a rational function. The polynomials occurring in the numerator and denominator are essentially the characteristic polynomials of the map induced by
on the various homology spaces.Connections
This generating function is essentially an algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic form of the Artin–Mazur zeta-function, which gives geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
information about the fixed and periodic points of ƒ.
See also
- Lefschetz fixed point theorem
- Artin–Mazur zeta-function