Legendrian knot
Encyclopedia
In mathematics
, a Legendrian knot often refers to a smooth embedding of the circle into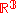
, which is tangent to the standard contact structure on 
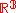. It is the lowest dimensional case of a Legendrian submanifold, which is an embedding of a k-dimensional manifold into a (2k+1)-dimensional that is always tangent to the contact hyperplane.
There can be inequivalent Legendrian knots that are isotopic as topological knots. These can be detected by considering their Thurston-Bennequin invariants and rotation number
, which are together known as the "classical invariants" of Legendrian knots. There are also more sophisticated invariants of Legendrian knots constructed combinatorially by Chekanov and using holomorphic discs by Eliashberg. This Chekanov-Eliashberg invariant yields an invariant for loops of Legendrian knots by considering the monodromy of the loops. This has yielded noncontractible loops of Legendrian knots which are contractible in the space of all knots.
Any Legendrian knot may be C^0 perturbed to a transverse knot
by pushing off in a direction transverse to the contact planes. The set of isomorphism classes of Legendrian knots modulo negative Legendrian stabilizations is in bijection with the set of transverse knots.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Legendrian knot often refers to a smooth embedding of the circle into
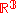, which is tangent to the standard contact structure on 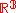. It is the lowest dimensional case of a Legendrian submanifold, which is an embedding of a k-dimensional manifold into a (2k+1)-dimensional that is always tangent to the contact hyperplane.There can be inequivalent Legendrian knots that are isotopic as topological knots. These can be detected by considering their Thurston-Bennequin invariants and rotation number
Rotation number
In mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...
, which are together known as the "classical invariants" of Legendrian knots. There are also more sophisticated invariants of Legendrian knots constructed combinatorially by Chekanov and using holomorphic discs by Eliashberg. This Chekanov-Eliashberg invariant yields an invariant for loops of Legendrian knots by considering the monodromy of the loops. This has yielded noncontractible loops of Legendrian knots which are contractible in the space of all knots.
Any Legendrian knot may be C^0 perturbed to a transverse knot
Transverse knot
In mathematics, a transverse knot is a smooth embedding of a circle into a three-dimensional contact manifold such that the tangent vector at every point of the knot is transverse to the contact plane at that point....
by pushing off in a direction transverse to the contact planes. The set of isomorphism classes of Legendrian knots modulo negative Legendrian stabilizations is in bijection with the set of transverse knots.