Leslie matrix
Encyclopedia
In applied mathematics
, the Leslie matrix is a discrete
, age-structured model of population growth
that is very popular in population ecology
. It was invented by and named after Patrick H. Leslie. The Leslie matrix
(also called the Leslie Model) is one of the best known ways to describe the growth of populations (and their projected age distribution), in which a population is closed to migration and where only one sex, usually the female
, is considered.
The Leslie Matrix is used in ecology
to model the changes in a population of organisms over a period of time. In a Leslie Model, the population is divided into groups based on age classes. A similar model which replaces age classes with life stage is called a Lefkovitch matrix, whereby individuals can both remain in the same stage class or move on to the next one. At each time step the population is represented by a vector with an element for each age classes where each element indicates the number of individuals currently in that class.
The Leslie Matrix is a square matrix
with the same number of rows and columns as the population vector has elements. The (i,j)th cell in the matrix indicates how many individuals will be in the age class i at the next time step for each individual in stage j. At each time step, the population vector is multiplied by the Leslie Matrix to generate the population vector for the following time step.
To build a matrix, some information must be known from the population:
The observations that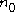
at time t+1 is simply the sum of all offspring born from the previous time step and that the organisms surviving to time t+1 are the organisms at time t surviving at probability 
we get 
This then motivates the following matrix representation:
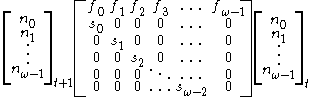
Where
is the maximum age attainable in our population.
This can be written as;
or;
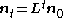
Where
is the population vector at time t and 
is the Leslie matrix.
The characteristic polynomial
of the matrix is given by the Euler–Lotka equation.
The Leslie model is very similar to a discrete-time Markov chain
. The main difference
is that in a Markov model, one would have
for each 
,
while the Leslie model may have these sums greater or less than 1.
, or age distribution, the population tends asymptotically to this age-structure and growth rate. It also returns to this state following perturbation. The Euler–Lotka equation provides a means of identifying the intrinsic growth rate. The stable age-structure is determined both by the growth rate and the survival function (i.e. the Leslie matrix). For example, a population with a large intrinsic growth rate will have a disproportionately “young” age-structure. A population with high mortality rates at all ages (i.e. low survival) will have a similar age-structure. Charlesworth (1980) provides further details on the rate and form of convergence to the stable age-structure.
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, the Leslie matrix is a discrete
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
, age-structured model of population growth
Population growth
Population growth is the change in a population over time, and can be quantified as the change in the number of individuals of any species in a population using "per unit time" for measurement....
that is very popular in population ecology
Population ecology
Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment. It is the study of how the population sizes of species living together in groups change over time and space....
. It was invented by and named after Patrick H. Leslie. The Leslie matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(also called the Leslie Model) is one of the best known ways to describe the growth of populations (and their projected age distribution), in which a population is closed to migration and where only one sex, usually the female
Female
Female is the sex of an organism, or a part of an organism, which produces non-mobile ova .- Defining characteristics :The ova are defined as the larger gametes in a heterogamous reproduction system, while the smaller, usually motile gamete, the spermatozoon, is produced by the male...
, is considered.
The Leslie Matrix is used in ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
to model the changes in a population of organisms over a period of time. In a Leslie Model, the population is divided into groups based on age classes. A similar model which replaces age classes with life stage is called a Lefkovitch matrix, whereby individuals can both remain in the same stage class or move on to the next one. At each time step the population is represented by a vector with an element for each age classes where each element indicates the number of individuals currently in that class.
The Leslie Matrix is a square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with the same number of rows and columns as the population vector has elements. The (i,j)th cell in the matrix indicates how many individuals will be in the age class i at the next time step for each individual in stage j. At each time step, the population vector is multiplied by the Leslie Matrix to generate the population vector for the following time step.
To build a matrix, some information must be known from the population:
-
, the number of individual (n) of each age class x
-
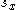, the fraction of individuals that survives from age class x to age class x+1,
-
, fecundityFecundityFecundity, derived from the word fecund, generally refers to the ability to reproduce. In demography, fecundity is the potential reproductive capacity of an individual or population. In biology, the definition is more equivalent to fertility, or the actual reproductive rate of an organism or...
, the per capitaPer capitaPer capita is a Latin prepositional phrase: per and capita . The phrase thus means "by heads" or "for each head", i.e. per individual or per person...
average number of female offspring reaching
born from mother of the age class x More precisely it can be viewed as the number of offspring produced at the next age class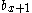 
weighted by the probability of reaching the next age class. Therefore 
The observations that
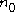at time t+1 is simply the sum of all offspring born from the previous time step and that the organisms surviving to time t+1 are the organisms at time t surviving at probability we get This then motivates the following matrix representation: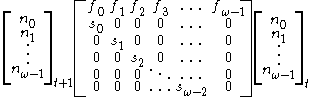Where
is the maximum age attainable in our population.This can be written as;
or;
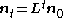
Where
is the population vector at time t and is the Leslie matrix.The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the matrix is given by the Euler–Lotka equation.
The Leslie model is very similar to a discrete-time Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
. The main difference
is that in a Markov model, one would have
for each ,while the Leslie model may have these sums greater or less than 1.
Stable age structure
This age-structured growth model suggests a steady-state, or stable, age-structure and growth rate. Regardless of the initial population size,, or age distribution, the population tends asymptotically to this age-structure and growth rate. It also returns to this state following perturbation. The Euler–Lotka equation provides a means of identifying the intrinsic growth rate. The stable age-structure is determined both by the growth rate and the survival function (i.e. the Leslie matrix). For example, a population with a large intrinsic growth rate will have a disproportionately “young” age-structure. A population with high mortality rates at all ages (i.e. low survival) will have a similar age-structure. Charlesworth (1980) provides further details on the rate and form of convergence to the stable age-structure.