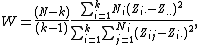Levene's test
Encyclopedia
In statistics
, Levene's test is an inferential statistic used to assess the equality of variance
s in different samples. Some common statistical procedures assume that variances of the populations from which different samples are drawn are equal. Levene's test assesses this assumption. It tests the null hypothesis
that the population variances are equal (called homogeneity of variance). If the resulting p-value of Levene's test is less than some critical value (typically 0.05), the obtained differences in sample variances are unlikely to have occurred based on random sampling. Thus, the null hypothesis of equal variances is rejected and it is concluded that there is a difference between the variances in the population.
Procedures which typically assume homogeneity of variance include analysis of variance
and t-tests
.
One advantage of Levene's test is that it does not require normality of the underlying data.
Levene's test is often used before a comparison of means. When Levene's test is significant, modified procedures are used that do not assume equality of variance.
Levene's test may also test a meaningful question in its own right if a researcher is interested in knowing whether population group variances are different.
where
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Levene's test is an inferential statistic used to assess the equality of variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s in different samples. Some common statistical procedures assume that variances of the populations from which different samples are drawn are equal. Levene's test assesses this assumption. It tests the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that the population variances are equal (called homogeneity of variance). If the resulting p-value of Levene's test is less than some critical value (typically 0.05), the obtained differences in sample variances are unlikely to have occurred based on random sampling. Thus, the null hypothesis of equal variances is rejected and it is concluded that there is a difference between the variances in the population.
Procedures which typically assume homogeneity of variance include analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
and t-tests
Student's t-test
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
.
One advantage of Levene's test is that it does not require normality of the underlying data.
Levene's test is often used before a comparison of means. When Levene's test is significant, modified procedures are used that do not assume equality of variance.
Levene's test may also test a meaningful question in its own right if a researcher is interested in knowing whether population group variances are different.
Definition
The test statistic, W, is defined as follows:where
-
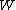 is the result of the test,
is the result of the test, -
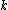 is the number of different groups to which the samples belong,
is the number of different groups to which the samples belong, -
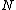 is the total number of samples,
is the total number of samples, -
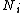 is the number of samples in the
is the number of samples in the 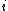 th group,
th group, -
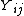 is the value of the
is the value of the 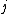 th sample from the
th sample from the  th group,
th group, -
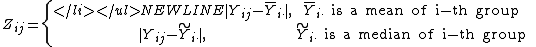
(Both definitions are in use though the second one is, strictly speaking, the Brown–Forsythe test – see below for comparison)-
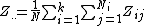 is the mean of all
is the mean of all 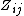 ,
, -
 is the mean of the
is the mean of the 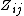 for group
for group 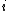 .
.
The significance of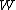 is tested against
is tested against 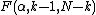 where
where  is a quantile of the F test distribution, with
is a quantile of the F test distribution, with 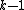 and
and  its degrees of freedom, and
its degrees of freedom, and  is the chosen level of significance (usually 0.05 or 0.01).
is the chosen level of significance (usually 0.05 or 0.01).
Comparison with the Brown–Forsythe test
The Brown–Forsythe test uses the median instead of the mean. Although the optimal choice depends on the underlying distribution, the definition based on the median is recommended as the choice that provides good robustnessRobust statisticsRobust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
against many types of non-normal data while retaining good statistical powerStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
. If one has knowledge of the underlying distribution of the data, this may indicate using one of the other choices. Brown and Forsythe performed Monte CarloMonte CarloMonte Carlo is an administrative area of the Principality of Monaco....
studies that indicated that using the trimmed mean performed best when the underlying data followed a Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
(a heavy-tailed distribution) and the median performed best when the underlying data followed a Chi-squared distribution with four degrees of freedom (a heavily skewed distributionSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
). Using the mean provided the best power for symmetric, moderate-tailed, distributions. -