Levi-Civita field
Encyclopedia
In mathematics, the Levi-Civita field, named after Tullio Levi-Civita
, is a non-Archimedean ordered field
, i.e., a system of numbers containing infinite and infinitesimal
quantities. Its members can be constructed as formal series of the form
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
, is a non-Archimedean ordered field
Non-Archimedean ordered field
In mathematics, a non-Archimedean ordered field is an ordered field that does not satisfy the Archimedean property. Examples are the Levi-Civita field, the hyperreal numbers, the surreal numbers, the Dehn field, and the field of rational functions with real coefficients with a suitable...
, i.e., a system of numbers containing infinite and infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
quantities. Its members can be constructed as formal series of the form
-
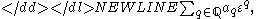
where
are real numbers, 
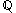is the set of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, and
is to be interpreted as a positive infinitesimal. The set of indices of the nonvanishing coefficients 
must be a left-finite set, i.e., for any member of the set, there are only finitely many members less than it; this restriction is necessary in order to make multiplication and division well defined and unique. The ordering is defined according to dictionary ordering of the list of coefficients, which is equivalent to the assumption that 
is an infinitesimal.
The real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are embedded in this field as series in which all of the coefficients vanish except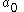
.
Examples
-
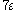is an infinitesimal that is greater than 
, but less than every positive real number. -
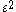is less than 
, and is also less than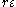 
for any positive real 
. -
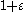differs infinitesimally from 1. -
is greater than 
, but still less than every positive real number. -
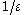is greater than any real number. -
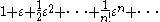is interpreted as 
. -
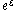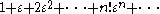is a valid member of the field, because the series is to be construed formally, without any consideration of convergence.
Extensions and applications
The field can be algebraically closedAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
by adjoining an imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
(i), or by letting the coefficients be complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. It is rich enough to allow a significant amount of analysis to be done, but its elements can still be represented on a computer in the same sense that real numbers can be represented using floating pointFloating pointIn computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
. It is the basis of automatic differentiationAutomatic differentiationIn mathematics and computer algebra, automatic differentiation , sometimes alternatively called algorithmic differentiation, is a set of techniques to numerically evaluate the derivative of a function specified by a computer program...
, a way to perform differentiation in cases that are intractable by symbolic differentiation or finite-difference methods.
Hahn seriesHahn seriesIn mathematics, Hahn series are a type of formal infinite series. They are a generalization of Puiseux series and were first introduced by Hans Hahn in 1907...
(with real coefficients and value group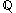
) are a larger field which relaxes the condition on the support 
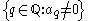of being left finite to that of being well-orderedWell-orderIn mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
(i.e., admitting no decreasing sequence): this gives a meaning to series such as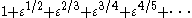
which are not in the Levi-Civita field.
External links
-