
Lexicographic order topology on the unit square
Encyclopedia
In mathematics, and especially general topology
, the lexicographic ordering on the unit square is an example of a topology
on the unit square S, i.e. on the set of points (x,y) in the plane such that and To give S a topology means to say which subset
s of S are "open", and to do so in a way that the following axiom
s are met:
This is an example of an order topology
in which there are uncountably many pairwise disjoint homeomorphic copies of the real line.
ing on the square to define a topology. Given two points in the square, say (x,y) and (u,v), we say that if and only if either or both and .
Given the lexicographical ordering on the square, we use the order topology to define the topology on S. For each point (u,v) we get an open set, denoted Uu,v, given by all the points in S that precede (u,v) with respect to the lexicographical ordering: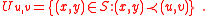
The open sets in the lexicographic ordering on the unit square are the whole set S, the empty set ∅, and those sets generated by the Uu,v, i.e. the sets formed by all possible unions of finite intersections.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, the lexicographic ordering on the unit square is an example of a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the unit square S, i.e. on the set of points (x,y) in the plane such that and To give S a topology means to say which subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of S are "open", and to do so in a way that the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s are met:
- The union of open sets is an open set.
- The finite intersection of open sets is an open set.
- S and the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅ are open sets.
This is an example of an order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
in which there are uncountably many pairwise disjoint homeomorphic copies of the real line.
Construction
As the name suggests, we use the lexicographical orderLexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
ing on the square to define a topology. Given two points in the square, say (x,y) and (u,v), we say that if and only if either or both and .
Given the lexicographical ordering on the square, we use the order topology to define the topology on S. For each point (u,v) we get an open set, denoted Uu,v, given by all the points in S that precede (u,v) with respect to the lexicographical ordering:
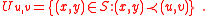
The open sets in the lexicographic ordering on the unit square are the whole set S, the empty set ∅, and those sets generated by the Uu,v, i.e. the sets formed by all possible unions of finite intersections.

