
Li's criterion
Encyclopedia
In number theory
, Li's criterion is a particular statement about the positivity of a certain sequence that is completely equivalent to the Riemann hypothesis
. The criterion is named after Xian-Jin Li, who presented it in 1997. Recently, Enrico Bombieri
and Jeffrey C. Lagarias provided a generalization, showing that Li's positivity condition applies to any collection of points that lie on the Re s = 1/2 axis.
is given by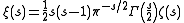
where ζ is the Riemann zeta function. Consider the sequence
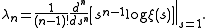
Li's criterion is then the statement that
The numbers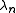 may also be expressed in terms of the non-trivial zeros of the Riemann zeta function:
may also be expressed in terms of the non-trivial zeros of the Riemann zeta function:
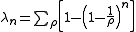
where the sum extends over ρ, the non-trivial zeros of the zeta function. This conditionally convergent sum should be understood in the sense that is usually used in number theory, namely, that

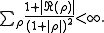
Then one may make several equivalent statements about such a set. One such statement is the following:
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Li's criterion is a particular statement about the positivity of a certain sequence that is completely equivalent to the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. The criterion is named after Xian-Jin Li, who presented it in 1997. Recently, Enrico Bombieri
Enrico Bombieri
Enrico Bombieri is a mathematician who has been working at the Institute for Advanced Study in Princeton, New Jersey. Bombieri's research in number theory, algebraic geometry, and mathematical analysis have earned him many international prizes --- a Fields Medal in 1974 and the Balzan Prize in 1980...
and Jeffrey C. Lagarias provided a generalization, showing that Li's positivity condition applies to any collection of points that lie on the Re s = 1/2 axis.
Definition
The Riemann ξ functionRiemann Xi function
In mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation...
is given by
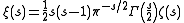
where ζ is the Riemann zeta function. Consider the sequence
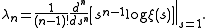
Li's criterion is then the statement that
- the Riemann hypothesis is completely equivalent to the statement that
 for every positive integer n.
for every positive integer n.
The numbers
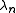 may also be expressed in terms of the non-trivial zeros of the Riemann zeta function:
may also be expressed in terms of the non-trivial zeros of the Riemann zeta function: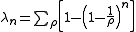
where the sum extends over ρ, the non-trivial zeros of the zeta function. This conditionally convergent sum should be understood in the sense that is usually used in number theory, namely, that

A generalization
Bombieri and Lagarias demonstrate that a similar criterion holds for any collection of complex numbers, and is thus not restricted to the Riemann hypothesis. More precisely, let R = {ρ} be any collection of complex numbers ρ, not containing ρ = 1, which satisfies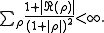
Then one may make several equivalent statements about such a set. One such statement is the following:
- One has
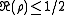 for every ρ if and only if
for every ρ if and only if

for all positive integers n.
One may make a more interesting statement, if the set R obeys a certain functional equationFunctional equationIn mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
under the replacement s ↦ 1 − s. Namely, if, whenever ρ is in R, then both the complex conjugate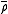 and
and 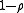 are in R, then Li's criterion can be stated as:
are in R, then Li's criterion can be stated as:
- One has Re(ρ) = 1/2 for every ρ if and only if
Bombieri and Lagarias also show that Li's criterion follows from Weil's criterionWeil's criterionIn mathematics, Weil's criterion is a criterion of André Weil for the Generalized Riemann Hypothesis to be true. It takes the form of an equivalent statement, to the effect that a certain generalized function is positive definite....
for the Riemann hypothesis.


