Riemann Xi function
Encyclopedia
In mathematics
, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation
. The function is named in honour of Bernhard Riemann
.
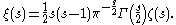
The functional equation (or reflection formula
) for the xi is
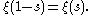
The upper-case Xi function is defined as
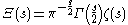
and of course obeys the same functional equation.
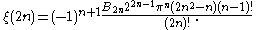
For example:
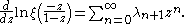
This expansion plays a particularly important role in Li's criterion
, which states that the Riemann hypothesis
is equivalent to having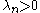
for all positive n.
As pointed by several works by Alain Connes
and others, the Riemann hypothesis
is equivalent to the assertion that the Riemann xi function is the functional determinant of the operator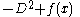
with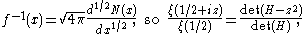
this conjecture is supported by several numerical evaluations
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
. The function is named in honour of Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
.
Definition
Riemann's lower-case xi is defined as: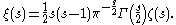The functional equation (or reflection formula
Reflection formula
In mathematics, a reflection formula or reflection relation for a function f is a relationship between f and f...
) for the xi is
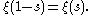
The upper-case Xi function is defined as
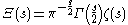
and of course obeys the same functional equation.
Values
The general form for even integers is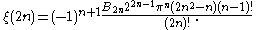For example:
Series representations
The xi function has the series expansion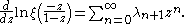This expansion plays a particularly important role in Li's criterion
Li's criterion
In number theory, Li's criterion is a particular statement about the positivity of a certain sequence that is completely equivalent to the Riemann hypothesis. The criterion is named after Xian-Jin Li, who presented it in 1997. Recently, Enrico Bombieri and Jeffrey C...
, which states that the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is equivalent to having
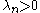for all positive n.Riemann Hypothesis
(This contribution is interesting yet completely unintelligible. The operators D, N, H and z have not been defined, neither has the functional space over which the determinant operates. Even if the reader is interested, no source material is provided to support these "claims" (technically, nothing has been claimed until the symbols have meaning, which they haven't.))As pointed by several works by Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and others, the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is equivalent to the assertion that the Riemann xi function is the functional determinant of the operator
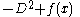
with
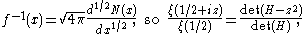
this conjecture is supported by several numerical evaluations