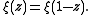Reflection formula
Encyclopedia
In mathematics
, a reflection formula or reflection relation for a function
f is a relationship between f(a − x) and f(x). It is a special case of a functional equation
, and it is very common in the literature to use the term "functional equation" when "reflection formula" is meant.
Reflection formulas are useful for numerical computation
of special functions. In effect, an approximation that has greater accuracy or only converges on one side of a reflection point (typically in the positive half of the complex plane
) can be employed for all arguments.
satisfy simple reflection relations around a = 0. For all even functions,
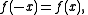
and for all odd functions,

A famous relationship is Euler's reflection formula
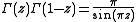
for the Gamma function
Γ(z), due to Leonhard Euler
.
There is also a reflection formula for the general nth order polygamma function ψn(z),
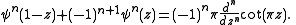
The Riemann zeta function ζ(z) satisfies
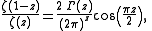
and the Riemann Xi function
ξ(z) satisfies
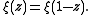
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a reflection formula or reflection relation for a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f is a relationship between f(a − x) and f(x). It is a special case of a functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
, and it is very common in the literature to use the term "functional equation" when "reflection formula" is meant.
Reflection formulas are useful for numerical computation
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
of special functions. In effect, an approximation that has greater accuracy or only converges on one side of a reflection point (typically in the positive half of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
) can be employed for all arguments.
Known formulae
The even and odd functionsEven and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
satisfy simple reflection relations around a = 0. For all even functions,
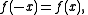
and for all odd functions,

A famous relationship is Euler's reflection formula
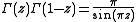
for the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
Γ(z), due to Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
.
There is also a reflection formula for the general nth order polygamma function ψn(z),
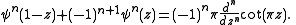
The Riemann zeta function ζ(z) satisfies
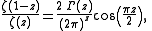
and the Riemann Xi function
Riemann Xi function
In mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation...
ξ(z) satisfies