
Lifting theory
Encyclopedia
Lifting theory was first introduced in a series of pioneering papers by John von Neumann
. A lifting on a measure space is a linear and multiplicative inverse
is a linear and multiplicative inverse
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
. A lifting on a measure space
 is a linear and multiplicative inverse
is a linear and multiplicative inverse-

of the quotient map
-
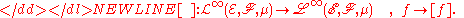
In other words, a lifting picks from every equivalence class
of bounded measurable functions modulo negligible functions
a representative
— which is henceforth written
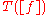
or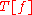
or simply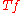 —
—
in such a way that-

-

-
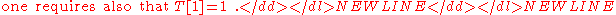
Liftings are used to produce
disintegrations of measuresDisintegration theoremIn mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
,
for instance
conditional probability distributions
given continuous random variables, and fibrations of Lebesgue measure on the
level sets of a function.
Existence of liftings
Theorem. Suppose
is complete.
Then admits a lifting
admits a lifting
if and only if there exists a collection of mutually
disjoint integrable sets in
whose union is .
.
In particular, if is the
is the
completion of a sigma-finite
measure or of an inner regular Borel measure on a locally compact space,
then admits a lifting.
admits a lifting.
The proof consists in extending a lifting to ever larger sub-sigma-algebras,
applying Doob's martingale convergence theoremDoob's martingale convergence theoremsIn mathematics — specifically, in stochastic analysis — Doob's martingale convergence theorems are a collection of results on the long-time limits of supermartingales, named after the American mathematician Joseph Leo Doob....
if one encounters a countable chain in the process.
Strong liftings
Suppose now that is complete
is complete
and that
comes equipped with a completely regular Hausdorff topology
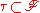
such that the union of any collection of negligible open sets
is again negligible – this is the case if
 is sigma-finite or comes from a
is sigma-finite or comes from a
Radon measure.
Then the support of ,
,
 ,
,
can be defined as the complement of the largest negligible open subset,
and the collection
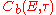
of bounded continuous functions belongs to
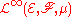 .
.
A strong lifting for
 is a lifting
is a lifting

such that
on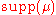 for all
for all
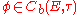 .
.
This is the same as requiring that
 for all open sets
for all open sets
 .
.
Theorem. If
is sigma-finite and complete
and
has a countable basis then

admits a strong lifting.
Proof. Let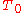 be a lifting for
be a lifting for
 and
and
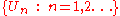 a countable basis for
a countable basis for
 .
.
For any point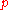 in the negligible set
in the negligible set

let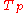 be any character
be any character
on
that extends the character

of .
.
Then define, for
and ,
,
-

 is the desired strong lifting.
is the desired strong lifting.
Application: disintegration of a measure
Suppose
and
are sigma-finite measure spaces (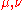 positive)
positive)
and is a measurable map.
is a measurable map.
A disintegration of
along
with respect to
is a slew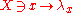
of positive sigma-additive measures on

such that (1)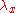
is carried by the fiber
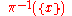
of
over :
:
-
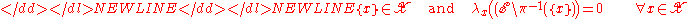
and (2) for every -integrable
-integrable
function ,
,
-
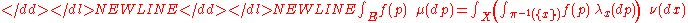 (*)
(*)
in the sense that, for
 -almost all
-almost all
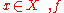
is -integrable,
-integrable,
the function

is -integrable,
-integrable,
and the displayed equality (*) obtains.
DisintegrationsDisintegration theoremIn mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
exist in various circumstances,
the proofs varying but almost all using strong liftings.
Here is a rather general result.
Its short proof gives the general flavor.
Theorem.
Suppose is a polish
is a polish
space and
a separable Hausdorff space, both equipped with their Borel sigma-algebras.
Let be a
be a
sigma-finite Borel measure on
and
an –measurable map.
–measurable map.
Then there exists a sigma-finite Borel measure

on
and a disintegration (*).
If is finite,
is finite,
 can be taken to
can be taken to
be the pushforward
 ,
,
and then the
are probabilities.
Proof.
Because of the polish nature of
there is a sequence of compact subsets of
that are mutually disjoint, whose union has negligible complement,
and on which is continuous.
is continuous.
This observation reduces the problem to the case that
both
and are compact and
are compact and
 is continuous, and
is continuous, and
 .
.
Complete under
under
 and
and
fix a strong lifting
for .
.
Given a bounded -measurable function
-measurable function
 ,
,
let denote
denote
its conditional expectation under ,
,
i.e., the Radon-Nikodym derivativeRadon–Nikodym theoremIn mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
of

with respect to .
.
Then set, for every ,
,

To show that this defines a disintegration is a matter of bookkeeping
and a suitable Fubini theorem.
To see how the strongness of the lifting enters, note
that-

and take the infimum over all positive
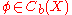
with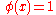 ;
;
it becomes apparent that the support of
lies in the fiber over .
.
-
-
-
-
-
-
-
-

