
Limiting cases of Apollonius' problem
Encyclopedia
In Euclidean geometry
, Apollonius' problem is to construct all the circles that are tangent to three given circles. Limiting cases of Apollonius' problem are those in which at least one of the given circles is a point or line, i.e., is a circle of zero or infinite radius. There are nine types of such limiting cases of Apollonius' problem, namely, to construct the circles tangent to:
In a different type of limiting case, the three given geometrical elements may have a special arrangement, such as constructing a circle tangent to two given parallel lines and one given circle.
, Euclidean geometry
is concerned with proofs of general truths from a minimum of postulates. For example, a simple proof would be to show that at least two of the angles of an isoceles triangle are equal. One important type of proof in Euclidean geometry is to show that a geometrical object can be constructed with a compass and an unmarked straightedge; an object can be constructed iff (something about no higher than square roots are taken). Therefore, it is important to determine whether an object can be constructed with compass and straightedge and, if so, how it may be constructed.
Euclid developed numerous constructions using compass and straightedge. Examples include: regular polygons such as the pentagon and hexagon, a line parallel to another that passes through a given point, etc. Many rose windows in Gothic cathedrals, as well as some Irish knot-work, can be designed using only Euclidean constructions. However, some geometrical constructions are simply impossible with those tools, including the heptagon and trisecting an angle.
Apollonius contributed a set of constructions, namely, finding the circles that are tangent to three geometrical elements simultaneously, where the "elements" may be a point, line or circle.
The initial elements in a geometric construction are called the "givens", such as a given point, a given line or a given circle.
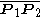 ,
, 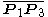 and
and 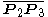 . At least two of these bisectors must intersect, and their intersection point is the center of the solution circle. The radius of the solution circle is the distance from that center to any one of the three given points.
. At least two of these bisectors must intersect, and their intersection point is the center of the solution circle. The radius of the solution circle is the distance from that center to any one of the three given points.
is the line connecting those two points. Consider the point G at which the radical axis intersects one of the two given lines. Since, every point on the radical axis has the same power relative to each circle, the distances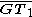 and
and 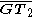 to the solution tangent points T1 and T2, are equal to each other and to the product
to the solution tangent points T1 and T2, are equal to each other and to the product
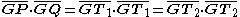
Thus, the distances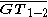 are both equal to the geometric mean
are both equal to the geometric mean
of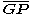 and
and  . From G and this distance, the tangent points T1 and T2 can be found. Then, the two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
. From G and this distance, the tangent points T1 and T2 can be found. Then, the two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
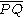 with L. In that case, the sole solution circle is the circle that passes through the three points P, Q and T.
with L. In that case, the sole solution circle is the circle that passes through the three points P, Q and T.
If the line l is not parallel to the given line L, then it intersects L at a point G. By the power of a point theorem, the distance from G to a tangent point T must equal the geometric mean
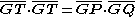
Two points on the given line L are located at a distance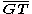 from the point G, which may be denoted as T1 and T2. The two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
from the point G, which may be denoted as T1 and T2. The two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, Apollonius' problem is to construct all the circles that are tangent to three given circles. Limiting cases of Apollonius' problem are those in which at least one of the given circles is a point or line, i.e., is a circle of zero or infinite radius. There are nine types of such limiting cases of Apollonius' problem, namely, to construct the circles tangent to:
- three points (denoted PPP, generally 1 solution)
- three lines (denoted LLL, generally 4 solutions)
- one line and two points (denoted LPP, generally 2 solutions)
- two lines and a point (denoted LLP, generally 2 solutions)
- one circle and two points (denoted CPP, generally 2 solutions)
- one circle, one line, and a point (denoted CLP, generally 4 solutions)
- two circles and a point (denoted CCP, generally 4 solutions)
- one circle and two lines (denoted CLL, generally 8 solutions)
- two circles and a line (denoted CCL, generally 8 solutions)
In a different type of limiting case, the three given geometrical elements may have a special arrangement, such as constructing a circle tangent to two given parallel lines and one given circle.
Historical introduction
Like most branches of mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
is concerned with proofs of general truths from a minimum of postulates. For example, a simple proof would be to show that at least two of the angles of an isoceles triangle are equal. One important type of proof in Euclidean geometry is to show that a geometrical object can be constructed with a compass and an unmarked straightedge; an object can be constructed iff (something about no higher than square roots are taken). Therefore, it is important to determine whether an object can be constructed with compass and straightedge and, if so, how it may be constructed.
Euclid developed numerous constructions using compass and straightedge. Examples include: regular polygons such as the pentagon and hexagon, a line parallel to another that passes through a given point, etc. Many rose windows in Gothic cathedrals, as well as some Irish knot-work, can be designed using only Euclidean constructions. However, some geometrical constructions are simply impossible with those tools, including the heptagon and trisecting an angle.
Apollonius contributed a set of constructions, namely, finding the circles that are tangent to three geometrical elements simultaneously, where the "elements" may be a point, line or circle.
Rules of Euclidean constructions
In Euclidean constructions, only five basic operations are allowed:- Draw a line through two given points
- Draw a circle through a given point with a given center
- Find the intersection point of two given lines
- Find the intersection points of two given circles
- Find the intersection points of a given line and a given circle
The initial elements in a geometric construction are called the "givens", such as a given point, a given line or a given circle.
Example 1: Perpendicular bisector
A common task is to construct the perpendicular bisector of the line segment between two endpoints. To do this, one draws two circles, each centered on an endpoint and passing through the other endpoint (operation #2). The intersection points of these two circles may be found (operation #4), and both are equidistant from the endpoints. The line drawn through them (operation #1) is the perpendicular bisector, being the locus of points equidistant from both endpoints.Example 2: Angle bisector
Another simple problem is to generate the line that bisects the angle between two given rays. We begin by drawing a circle of arbitrary radius centered on the intersection point P of the two given lines (operation #2). The intersection points T1 and T2 of this circle with the two given rays may be found (operation #5). Two circles of the same radius, centered on T1 and T2, intersect at two points, P and Q. The line drawn through P and Q (operation #1) is an angle bisector. For rays, there is only one angle bisector; for lines, however, there are two, perpendicular to one another.Preliminary results
A few basic results are helpful in solving different special cases of Apollonius' problem. The most basic is that a line and a point can be thought of as circles of infinitely large and infinitely small radius, respectively. A circle is tangent to a point if it passes through the point, and tangent to a line if they intersect at a single point P and if the line is perpendicular to a radius drawn from the circle's center to P.Tangent line to a circle from a given point
Draw semicircle centered on the midpoint between the center of the circle and the given pointScaling two circles while maintaining their tangency
If two circles are internally tangent, they remain so if their radii are increased or decreased by the same amount. Conversely, if two circles are externally tangent, they remain so if their radii are changed by the same amount in opposite directions, one increasing and the other decreasing.Type 1: Three points (PPP, generally 1 solution)
As shown above, if a circle passes through two given points P1 and P2, its center must lie somewhere on the perpendicular bisector line of the two points. Therefore, if the solution circle passes through three given points P1, P2 and P3, its center must lie on the perpendicular bisectors of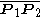 ,
, 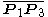 and
and 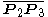 . At least two of these bisectors must intersect, and their intersection point is the center of the solution circle. The radius of the solution circle is the distance from that center to any one of the three given points.
. At least two of these bisectors must intersect, and their intersection point is the center of the solution circle. The radius of the solution circle is the distance from that center to any one of the three given points.Type 2: Three lines (LLL, generally 4 solutions)
As shown above, if a circle is tangent to two given lines, its center must lie on one of the two lines that bisect the angle between the two given lines. Therefore, if a circle is tangent to three given lines L1, L2, and L3, its center C must be located at the intersection of the bisecting lines of the three given lines. In general, there are four such points, giving four different solutions for the LLL Apollonius problem. The radius of each solution is determined by finding a point of tangency T, which may be done as follows. Choose one of the three intersection points P between the given lines; draw a circle centered on the midpoint of C and P of diameter equal to the distance between C and P. The intersections of that circle with the intersecting given lines are the two points of tangency.Type 3: One point, two lines (PLL, generally 2 solutions)
As shown above, if a circle is tangent to two given lines, its center must lie on one of the two lines that bisect the angle between the two given lines. By symmetry, if a such a circle passes through a given point P, it must also pass through a point Q that is the "mirror image" of P about the angle bisector. The two solution circles will pass through both P and Q, and their radical axisRadical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
is the line connecting those two points. Consider the point G at which the radical axis intersects one of the two given lines. Since, every point on the radical axis has the same power relative to each circle, the distances
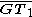 and
and 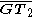 to the solution tangent points T1 and T2, are equal to each other and to the product
to the solution tangent points T1 and T2, are equal to each other and to the product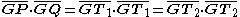
Thus, the distances
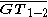 are both equal to the geometric mean
are both equal to the geometric meanGeometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of
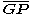 and
and  . From G and this distance, the tangent points T1 and T2 can be found. Then, the two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
. From G and this distance, the tangent points T1 and T2 can be found. Then, the two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.Type 4: Two points, one line (PPL, generally 2 solutions)
A line l may be drawn through the given points P and Q. If the line is parallel to the given line L, the tangent point T of the circle with L is located at the intersection of the perpendicular bisector of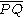 with L. In that case, the sole solution circle is the circle that passes through the three points P, Q and T.
with L. In that case, the sole solution circle is the circle that passes through the three points P, Q and T.If the line l is not parallel to the given line L, then it intersects L at a point G. By the power of a point theorem, the distance from G to a tangent point T must equal the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
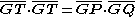
Two points on the given line L are located at a distance
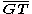 from the point G, which may be denoted as T1 and T2. The two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
from the point G, which may be denoted as T1 and T2. The two solution circles are the circles that pass through the three points (P, Q, T1) and (P, Q, T2), respectively.
