Radical axis - AbsoluteAstronomy.com

The radical axis of two circles is the locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles (orthogonally); conversely, the center of any circle that cuts both circles orthogonally must lie on the radical axis. In technical language, each point P on the radical axis has the same power

Power of a point

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...

with respect to both circles

where r₁ and r₂ are the radii of the two circles, d₁ and d₂ are distances from P to the centers of the two circles, and R is the radius of the unique orthogonal circle centered on P.

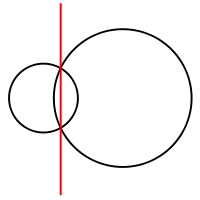
The radical axis is always a straight line and always perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

to the line connecting the centers of the circles, albeit closer to the circumference of the larger circle. If the circles intersect, the radical axis is the line passing through the intersection points; similarly, if the circles are tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

, the radical axis is simply the common tangent. In general, two disjoint, non-concentric circles can be aligned with the circles of bipolar coordinates

Bipolar coordinates

Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...

; in that case, the radical axis is simply the y-axis; every circle on that axis that passes through the two foci intersect the two circles orthogonally. Thus, two radii of such a circle are tangent to both circles, satisfying the definition of the radical axis. The collection of all circles with the same radical axis and with centers on the same line is known as a pencil

Pencil (mathematics)

A pencil in projective geometry is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a projective plane....

of coaxal circles.

Definition and general properties

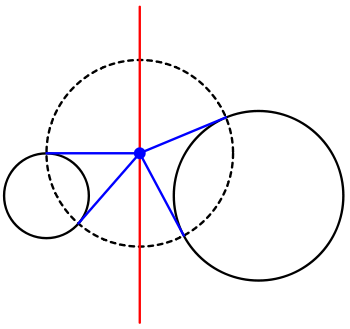
Radical center of three circles

Consider three circles A, B and C, no two of which are concentric. The radical axis theorem states that the three radical axes (for each pair of circles) intersect in one point called the radical center, or are parallel. In technical language, the three radical axes are concurrent (share a common point); if they are parallel, they concur at a point of infinity.

A simple proof is as follows. The radical axis of circles A and B is defined as the line along which the tangents to those circles are equal in length a=b. Similarly, the tangents to circles B and C must be equal in length on their radical axis. By the transitivity

Transitive relation

In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....

of equality, all three tangents are equal a=b=c at the intersection point r of those two radical axes. Hence, the radical axis for circles A and C must pass through the same point r, since a=c there. This common intersection point r is the radical center.

At the radical center, there is a unique circle that is orthogonal to all three circles. This follows because each radical axis is the locus of centers of circles that cut each pair of given circles orthogonally.

Geometric construction

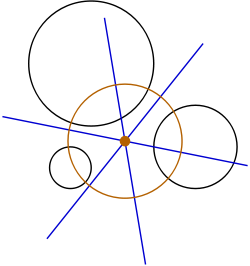
The radical axis of two circles A and B can be constructed by drawing a line through any two of its points. Such a point can be found by drawing a circle C that intersects both circles A and B in two points. The two lines passing through each pair of intersection points are the radical axes of A and C and of B and C. These two lines intersect in a point J that is the radical center of all three circles, as described above; therefore, this point also lies on the radical axis of A and B. Repeating this process with another such circle D provides a second point K. The radical axis is the line passing through both J and K.

A special case of this approach is carried out with antihomologous points from an internal or external center of similarity. Consider two rays emanating from an external homothetic center E. Let the anithomologous pairs of intersections points of these rays with the two given circles be denoted as P and Q, and S and T, respectively. These four points lie on a common circle that intersects the two given circles in two points each. Hence, the two lines joining P and S, and Q and T intersect at the radical center of the three circles, which lies on the radical axis of the given circles. Similarly, the line joining two antihomologous points on separate circles and their tangents form an isoceles triangle, with both tangents being of equal length. Therefore, such tangents meet on the radical axis.

Algebraic construction

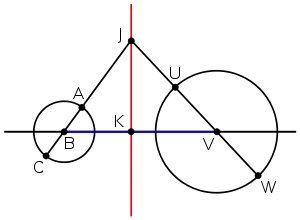
Referring to Figure 3, the radical axis (red) is perpendicular to the blue line segment joining the centers B and V of the two given circles, intersecting that line segment at a point K between the two circles. Therefore, it suffices to find the distance x₁ or x₂ from K to B or V, respectively, where x₁+x₂ equals D, the distance between B and V.

Consider a point J on the radical axis, and let its distances to B and V be denoted as d₁ and d₂, respectively. Since J must have the same power

Power of a point

with respect to both circles, it follows that

where r₁ and r₂ are the radii of the two given circles. By the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

, the distances d₁ and d₂ can be expressed in terms of x₁, x₂ and L, the distance from J to K

By cancelling L on both sides of the equation, the equation can be written

Dividing both sides by D = x₁+x₂ yields the equation

Adding this equation to x₁+x₂ = D yields a formula for x₁

Subtracting the same equation yields the corresponding formula for x₂

Determinant calculation

If the circles are represented in trilinear coordinates

Trilinear coordinates

In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...

in the usual way, then their radical center is conveniently given as a certain determinant. Specifically, let X = x : y : z denote a variable point in the plane of a triangle ABC with sidelengths a = |BC|, b = |CA|, c = |AB|, and represent the circles as follows:
(ax + by + cz) + g(ayz + bzx + cxy) = 0
(ax + by + cz) + k(ayz + bzx + cxy) = 0
(ax + by + cz) + p(ayz + bzx + cxy) = 0

Then the radical center is the point

External links

Animation at Cut-the-knot
Cut-the-knot
Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...