
Power of a point
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the power of a point is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
C of radius r is defined (Figure 1)

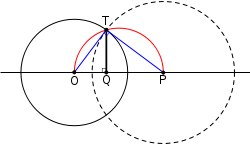
where s is the distance from P to the center O of the circle. By this definition, points inside the circle have negative power, points outside have positive power, and points on the circle have zero power. For external points, the power equals the square of the radius of a circle centered on the given point that intersects the given circle orthogonally, i.e., at right angles (Figure 2). The power of a point is also known as the point's circle power or the power of a circle with respect to the point.
The power of a point can be defined equivalently as the product of distances from the point P to the two intersection points of any ray emanating from P. For example, in Figure 1, a ray emanating from P intersects the circle in two points, M and N, whereas a tangent ray intersects the circle
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
in one point T; the horizontal ray from P intersects the circle at A and B, the endpoints of the diameter. Their respective products of distances are equal to each other and to the power of point P in that circle

This equality is sometimes known as the "secant-tangent theorem", "intersecting chords theorem", or the "power-of-a-point theorem".
The power of a point is used in many geometrical definitions and proofs. For example, the radical axis
Radical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
of two given circles is the straight line consisting of points that have equal power to both circles. For each point on this line, there is a unique circle centered on that point that intersects both given circles orthogonally; equivalently, tangents of equal length can be drawn from that point to both given circles. Similarly, the radical center of three circles is the unique point with equal power to all three circles. There exists a unique circle, centered on the radical center, that intersects all three given circles orthogonally, equivalently, tangents drawn from the radical center to all three circles have equal length.
Orthogonal circle
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
,

where s is again the distance from the point P to the center O of the given circle (solid black in Figure 2).
This construction of an orthogonal circle is useful in understanding the radical axis
Radical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
of two circles, and the radical center of three circles. The point T can be constructed—and, thereby, the radius R and the power p found geometrically—by finding the intersection of the given circle with a semicircle (red in Figure 2) centered on the midpoint of O and P and passing through both points. By simple geometry, it can also be shown that the point Q is the inverse of P with respect to the given circle.
Theorems
The power of a point theorem, due to Jakob SteinerJakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
, states that for any line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
through A intersecting C in points P and Q, the power of the point with respect to the circle is given up to a sign by the product

of the lengths of the segments from A to P and A to Q, with a positive sign if A is outside the circle and a negative sign otherwise: if A is on the circle, the product is zero. In the limiting case, when the line is tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the circle, P = Q, and the result is immediate from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
In the other two cases, when A is inside the circle, or A is outside the circle, the power of a point theorem has two corollaries
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
.
- The theorem of intersecting chords (or chord-chord power theorem) states that if A is a point in a circle and PQ and RS are chordsChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
of the circle intersecting at A, then
-
- The common value of these products is the negative of the power of the point A with respect to the circle.
- The theorem of intersecting secants (or secant-secant power theorem) states that if PQ and RS are chords of a circle which intersect at a point A outside the circle, then
- In this case the common value is the same as the power of A with respect to the circle.
- The tangent-secant theorem is a special case of the theorem of intersecting secants, where points Q and P coincide, i.e.
-
- This has utility in such applications as determining the distance to a point P on the horizonHorizonThe horizon is the apparent line that separates earth from sky, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting...
, by selecting points R and S to form a diameter chord, so that RS is the diameter of the planet, AR is the height above the planet, and AP is the distance to the horizon.
Darboux product
The power of a point is a special case of the Darboux product between two circles, which is given by
where A1 and A2 are the centers of the two circles and r1 and r2 are their radii. The power of a point arises in the special case that one of the radii is zero. If the two circles intersect, then their Darboux product is

where φ is the angle of intersection.
External links
- Jacob Steiner and the Power of a Point at Convergence
- Intersecting Chords Theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Intersecting Chords Theorem With interactive animation
- Intersecting Secants Theorem With interactive animation






