Tangent lines to circles
Encyclopedia
In Euclidean plane geometry
, tangent lines to circles form the subject of several theorem
s, and play an important role in many geometrical constructions and proofs
. Since the tangent line
to a circle
at a point
P is perpendicular
to the radius
to that point, theorems involving tangent lines often involve radial line
s and orthogonal
circles.
s the circle at a single point T. For comparison, secant line
s intersect a circle at two points, whereas another line may not intersect a circle at all. This property of tangent lines is preserved under many geometrical transformations, such as scalings
, rotation
, translations
, inversions, and map projections. In technical language, these transformations do not change the incidence structure
of the tangent line and circle, even though the line and circle may be deformed.
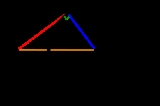
The radius of a circle is perpendicular to the tangent line through its endpoint on the circle's circumference. Conversely, the perpendicular to a radius through the same endpoint is a tangent line. The resulting geometrical figure of circle and tangent line has a reflection symmetry
about the axis of the radius.
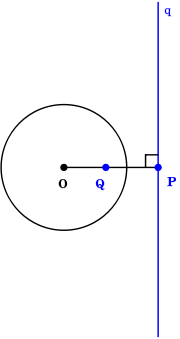
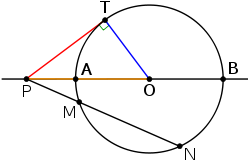No tangent line can be drawn through a point in the interior of a circle, since any such line must be a secant line. However, two tangent lines can be drawn to a circle from a point P outside of the circle. The geometrical figure of circle and both tangent lines likewise have a reflection symmetry about the radial axis joining P to the center point O of the circle. Thus length of the segments from P to the two tangent points are equal. By the secant-tangent theorem, the square of this tangent length equals the power of the point P
in the circle C. This power equals the product of distances from P to any two intersection points of the circle with a secant line passing through P.
The tangent line t and the tangent point T have a conjugate relationship to one another, which has been generalized into the idea of pole points and polar lines
. The same reciprocal relation exists between a point P outside the circle and the secant line joining its two points of tangency.
line to a. One method for constructing this perpendicular is as follows. Placing the compass point on T with the circle's radius r, a second point G is identified on the radial line a; thus, T is the midpoint of the line segment OG. Two intersecting circles of the same radius R>r are drawn, centered on O and G, respectively. The line drawn through their two points of intersection is the tangent line.
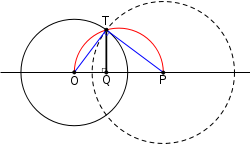Thales' theorem
may be used to construct the tangent lines to a point P external to the circle C. A circle is drawn centered on Q, the midpoint of the line segment OP, where O is again the center of the circle C. The intersection points T1 and T2 are the tangent points for lines passing through P, by the following argument. The line segments OT1 and OT2 are radii of the circle C; since both are inscribed in a semicircle, they are perpendicular to the line segments PT1 and PT2, respectively. But only a tangent line is perpendicular to the radial line. Hence, the two lines from P and passing through T1 and T2 are tangent to the circle C.
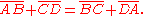
This conclusion follows from the equality of the tangent segments from the four points of the quadrilateral. Let the tangent points be denoted as P (on segment AB), Q (on segment BC), R (on segment CD) and S (on segment DA). The symmetric tangent segments about each point of ABCD are equal, e.g., BP=BQ=b, CQ=CR=c, DR=DS=d, and AS=AP=a.
But each side of the quadrilateral is composed of two such tangent segments
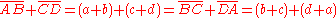
proving the theorem. The converse is also true: a circle can be inscribed into every quadrilateral in which the lengths of opposite sides sum to the same value.
This theorem has various uses. For example, it shows immediately that no rectangle can have an inscribed circle unless it is a square
, and that every rhombus has an inscribed circle, whereas a general parallelogram
does not.
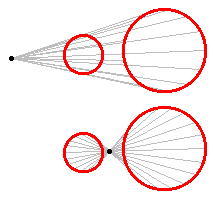For two circles, there are generally four bitangent
lines that are tangent to both. For two of these, the external tangent lines, the circles fall on the same side of the line; for the two others, the internal tangent lines, the circles fall on opposite sides of the line. The external tangent lines intersect in the external homothetic center
, whereas the internal tangent lines intersect at the internal homothetic center. The internal homothetic center always lies on the line joining the centers of the two circles, in the segment between the two circles. The exterior center lies on the same line, and is closer to the center of the smaller than to the center of the larger. If the two circles have equal radius, the external tangent lines are parallel, and — at least in inversive geometry — the external homothetic center, lies at infinity.
, with r1 > r2; in other words, circle C1 is defined as the larger of the two circles. Two different methods may be used to construct the external and internal tangent lines.
External tangents
A new circle C3 of radius r1 − r2 is drawn centered on O1. Using the method above, two lines are drawn from O2 that are tangent to this new circle. These lines are parallel to the desired tangent lines, because the situation corresponds to shrinking both circles C1 and C2 by a constant amount, r2, which shrinks C2 to a point. Two radial lines may be drawn from the center O1 through the tangent points on C3; these intersect C1 at the desired tangent points. The desired external tangent lines are the lines perpendicular to these radial lines at those tangent points, which may be constructed as described above.
Internal tangents
A new circle C3 of radius r1 + r2 is drawn centered on O1. Using the method above, two lines are drawn from O2 that are tangent to this new circle. These lines are parallel to the desired tangent lines, because the situation corresponds to shrinking C2 to a point while expanding C1 by a constant amount, r2. Two radial lines may be drawn from the center O1 through the tangent points on C3; these intersect C1 at the desired tangent points. The desired internal tangent lines are the lines perpendicular to these radial lines at those tangent points, which may be constructed as described above.
a*x + b*y = r where x = x2 - x1, y = y2 - y1 and r = r2 - r1 If d is the distance from c1 to c2 we can use X = x/d, Y = y/d and R = r/d to make things easier, a*X + b*Y = R and a2 + b2 = 1, solve these to get two solutions (k = +/-1).
a = R*X - k*Y*sqrt(1 - R2) This solution is beautiful. The unit vector (X,Y) points from c1 to c2.
b = R*Y + k*X*sqrt(1 - R2) The (unit) R matrices rotate it to point along the tangent lines.
c = r1 - (a*x1 + b*y1)
k = 1 is the tangent line to the right of the circles looking from c1 to c2.
k = -1 is the tangent line to the right of the circles looking from c2 to c1.
The above assumes each circle has +ve radius. If r1 is +ve and r2 -ve then c1 will lie to the left of each line and c2 to the right, and the two tangent lines will cross. In this way all 4 solutions are obtained.
, which is to calculate the length of a belt or rope needed to fit snugly over two pulleys. If the belt is considered to be a mathematical line of negligible thickness, and if both pulleys are assumed to lie in exactly the same plane, the problem devolves to summing the lengths of the relevant tangent line segments with the lengths of circular arcs subtended by the belt. If the belt is wrapped about the wheels so as to cross, the interior tangent line segments are relevant. Conversely, if the belt is wrapped exteriorly around the pulleys, the exterior tangent line segments are relevant; this case is sometimes called the pulley problem.
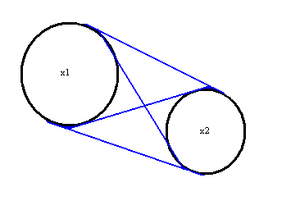In general the points of tangency t1 and t2 for the four lines tangent to two circles with centers x1 and x2 and radii r1 and r2 are given by solving the simultaneous equations:
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, tangent lines to circles form the subject of several theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s, and play an important role in many geometrical constructions and proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
. Since the tangent line
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
at a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
P is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
to that point, theorems involving tangent lines often involve radial line
Radial line
This article is about the mathematical concept. For the medical meaning, see arterial line.A radial line is a line passing through the center of a circle or sphere. The correct "direction" of the radial line is from the radius point to a point on the arc or circle. This applies to its use in...
s and orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
circles.
Tangent lines to one circle
A tangent line t to a circle C intersectLine-line intersection
In Euclidean geometry, the intersection of a line and a line can be the empty set,a point, ora line. Distinguishing these cases, and finding the intersection point have use, for example, in computer graphics, motion planning, and collision detection....
s the circle at a single point T. For comparison, secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
s intersect a circle at two points, whereas another line may not intersect a circle at all. This property of tangent lines is preserved under many geometrical transformations, such as scalings
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
, translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
, inversions, and map projections. In technical language, these transformations do not change the incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
of the tangent line and circle, even though the line and circle may be deformed.
The radius of a circle is perpendicular to the tangent line through its endpoint on the circle's circumference. Conversely, the perpendicular to a radius through the same endpoint is a tangent line. The resulting geometrical figure of circle and tangent line has a reflection symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
about the axis of the radius.
Power of a point
In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...
in the circle C. This power equals the product of distances from P to any two intersection points of the circle with a secant line passing through P.
Pole and polar
In geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...
. The same reciprocal relation exists between a point P outside the circle and the secant line joining its two points of tangency.
Geometrical constructions
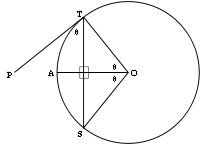
It is relatively straightforward to construct a line t tangent to a circle at a point T on the circumference of the circle. A line a is drawn from O, the center of the circle, through the radial point T; the line t is the perpendicularPerpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
line to a. One method for constructing this perpendicular is as follows. Placing the compass point on T with the circle's radius r, a second point G is identified on the radial line a; thus, T is the midpoint of the line segment OG. Two intersecting circles of the same radius R>r are drawn, centered on O and G, respectively. The line drawn through their two points of intersection is the tangent line.
Thales' theorem
In geometry, Thales' theorem states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem...
may be used to construct the tangent lines to a point P external to the circle C. A circle is drawn centered on Q, the midpoint of the line segment OP, where O is again the center of the circle C. The intersection points T1 and T2 are the tangent points for lines passing through P, by the following argument. The line segments OT1 and OT2 are radii of the circle C; since both are inscribed in a semicircle, they are perpendicular to the line segments PT1 and PT2, respectively. But only a tangent line is perpendicular to the radial line. Hence, the two lines from P and passing through T1 and T2 are tangent to the circle C.
Tangent quadrilateral theorem and inscribed circles
A tangent quadrilateral ABCD is a closed figure of four straight sides that are tangent to a given circle C. Equivalently, the circle C is inscribed in the quadrilateral ABCD. The sum of opposite sides of any such quadrilateral are equal, i.e.,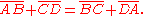But each side of the quadrilateral is composed of two such tangent segments
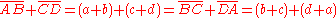
proving the theorem. The converse is also true: a circle can be inscribed into every quadrilateral in which the lengths of opposite sides sum to the same value.
This theorem has various uses. For example, it shows immediately that no rectangle can have an inscribed circle unless it is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, and that every rhombus has an inscribed circle, whereas a general parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
does not.
Tangent lines to two circles
Bitangent
In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
lines that are tangent to both. For two of these, the external tangent lines, the circles fall on the same side of the line; for the two others, the internal tangent lines, the circles fall on opposite sides of the line. The external tangent lines intersect in the external homothetic center
Homothetic center
In geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation/contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense...
, whereas the internal tangent lines intersect at the internal homothetic center. The internal homothetic center always lies on the line joining the centers of the two circles, in the segment between the two circles. The exterior center lies on the same line, and is closer to the center of the smaller than to the center of the larger. If the two circles have equal radius, the external tangent lines are parallel, and — at least in inversive geometry — the external homothetic center, lies at infinity.
Geometrical constructions
Let O1 and O2 be the centers of the two circles, C1 and C2 and let r1 and r2 be their radiiRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, with r1 > r2; in other words, circle C1 is defined as the larger of the two circles. Two different methods may be used to construct the external and internal tangent lines.
External tangents
A new circle C3 of radius r1 − r2 is drawn centered on O1. Using the method above, two lines are drawn from O2 that are tangent to this new circle. These lines are parallel to the desired tangent lines, because the situation corresponds to shrinking both circles C1 and C2 by a constant amount, r2, which shrinks C2 to a point. Two radial lines may be drawn from the center O1 through the tangent points on C3; these intersect C1 at the desired tangent points. The desired external tangent lines are the lines perpendicular to these radial lines at those tangent points, which may be constructed as described above.
Internal tangents
A new circle C3 of radius r1 + r2 is drawn centered on O1. Using the method above, two lines are drawn from O2 that are tangent to this new circle. These lines are parallel to the desired tangent lines, because the situation corresponds to shrinking C2 to a point while expanding C1 by a constant amount, r2. Two radial lines may be drawn from the center O1 through the tangent points on C3; these intersect C1 at the desired tangent points. The desired internal tangent lines are the lines perpendicular to these radial lines at those tangent points, which may be constructed as described above.
Algebraic solutions
Let the circles have centres c1 = (x1,y1) and c2 = (x2,y2) with radius r1 and r2 respectively. If the tangent line is (a,b,c) where a2 + b2 = 1 then a*x1 + b*y1 + c = r1 and a*x2 + b*y2 + c = r2 and we subtract the first from the second to geta*x + b*y = r where x = x2 - x1, y = y2 - y1 and r = r2 - r1 If d is the distance from c1 to c2 we can use X = x/d, Y = y/d and R = r/d to make things easier, a*X + b*Y = R and a2 + b2 = 1, solve these to get two solutions (k = +/-1).
a = R*X - k*Y*sqrt(1 - R2) This solution is beautiful. The unit vector (X,Y) points from c1 to c2.
b = R*Y + k*X*sqrt(1 - R2) The (unit) R matrices rotate it to point along the tangent lines.
c = r1 - (a*x1 + b*y1)
k = 1 is the tangent line to the right of the circles looking from c1 to c2.
k = -1 is the tangent line to the right of the circles looking from c2 to c1.
The above assumes each circle has +ve radius. If r1 is +ve and r2 -ve then c1 will lie to the left of each line and c2 to the right, and the two tangent lines will cross. In this way all 4 solutions are obtained.
Belt problem
The internal and external tangent lines are useful in solving the belt problemBelt problem
The belt problem is a mathematics problem which requires finding the length of a crossed belt that connects two circular pulleys with radius r1 and r2 whose centers are separated by a distance P...
, which is to calculate the length of a belt or rope needed to fit snugly over two pulleys. If the belt is considered to be a mathematical line of negligible thickness, and if both pulleys are assumed to lie in exactly the same plane, the problem devolves to summing the lengths of the relevant tangent line segments with the lengths of circular arcs subtended by the belt. If the belt is wrapped about the wheels so as to cross, the interior tangent line segments are relevant. Conversely, if the belt is wrapped exteriorly around the pulleys, the exterior tangent line segments are relevant; this case is sometimes called the pulley problem.
Illustration
-
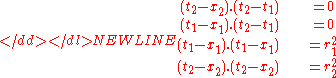
Outer tangent
The red line joining the points (x3,y3) and (x4,y4) is the outer tangent between the two circles. Given points (x1,y1), (x2,y2) the points (x3,y3), (x4,y4) can easily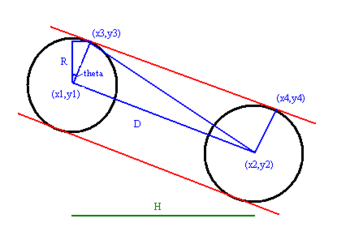
be calculated by equating the angle theta and adding the x,y coordinates of the triangle(theta) to the original coordinates (x1,y1) as shown in the figure.
Inner tangent
An inner tangent is a tangent that intersects the segment joining two circles' centers. Note that the inner tangent will not be defined for cases when the two circles overlap.
Tangent lines to three circles: Monge's theorem
For three circles denoted by C1, C2, and C3, there are three pairs of circles (C1C2, C2C3, and C1C3). Since each pair of circles has two homothetic centers, there are six homothetic centerHomothetic centerIn geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation/contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense...
s altogether. Gaspard MongeGaspard MongeGaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...
showed in the early 19th century that these six points lie on four lines, each line having three collinear points.
Problem of Apollonius
Many special cases of Apollonius' problemProblem of ApolloniusIn Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
involve finding a circle that is tangent to one or more lines. The simplest of these is to construct circles that are tangent to three given lines (the LLL problem). To solve this problem, the center of any such circle must lie on an angle bisector of any pair of the lines; there are two angle-bisecting lines for every intersection of two lines. The intersections of these angle bisectors give the centers of solution circles. There are four such circles in general, the inscribed circle of the triangle formed by the intersection of the three lines, and the three exscribed circles.
A general Apollonius problem can be transformed into the simpler problem of circle tangent to one circle and two parallel lines (itself a special case of the LLC special case). To accomplish this, it suffices to scale
Scaling (geometry)In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
two of the three given circles until they just touch, i.e., are tangent. An inversion in their tangent point with respect to a circle of appropriate radius transforms the two touching given circles into two parallel lines, and the third given circle into another circle. Thus, the solutions may be found by sliding a circle of constant radius between two parallel lines until it contacts the transformed third circle. Re-inversion produces the corresponding solutions to the original problem.
Generalizations
The concept of a tangent line to one or more circles can be generalized in several ways. First, the conjugate relationship between tangent points and tangent lines can be generalized to pole points and polar linesPole and polarIn geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...
, in which the pole points may be anywhere, not only on the circumference of the circle. Second, the union of two circles is a special (reducible) case of a quartic plane curveQuartic plane curveA quartic plane curve is a plane curve of the fourth degree. It can be defined by a quartic equation:Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0....
, and the external and internal tangent lines are the bitangentBitangentIn mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
s to this quartic curve. A generic quartic curve has 28 bitangents.
A third generalization considers tangent circles, rather than tangent lines; a tangent line can be considered as a tangent circle of infinite radius. In particular, the external tangent lines to two circles are limiting cases of a family of circles which are internally or externally tangent to both circles, while the internal tangent lines are limiting cases of a family of circles which are internally tangent to one and externally tangent to the other of the two circles.
In Möbius or inversive geometry, lines are viewed as circles through a point "at infinity" and for any line and any circle, there is a Möbius transformation which maps one to the other. In Möbius geometry, tangency between a line and a circle becomes a special case of tangency between two circles. This equivalence is extended further in Lie sphere geometryLie sphere geometryLie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century...
.