
Quartic plane curve
Encyclopedia
A quartic plane curve is a plane curve
of the fourth degree. It can be defined by a quartic equation:
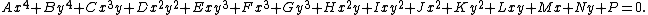
This equation has fifteen constants. However, it can be multiplied by any non-zero constant without changing the curve. Therefore, the space of quartic curves can be identified with the real projective space
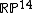 . It also follows that there is exactly one quartic curve that passes through a set of fourteen distinct points in general position
. It also follows that there is exactly one quartic curve that passes through a set of fourteen distinct points in general position
, since a quartic has 14 degrees of freedom
.
A quartic curve can have a maximum of:
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
of the fourth degree. It can be defined by a quartic equation:
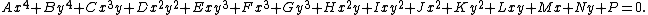
This equation has fifteen constants. However, it can be multiplied by any non-zero constant without changing the curve. Therefore, the space of quartic curves can be identified with the real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
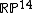 . It also follows that there is exactly one quartic curve that passes through a set of fourteen distinct points in general position
. It also follows that there is exactly one quartic curve that passes through a set of fourteen distinct points in general positionGeneral position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
, since a quartic has 14 degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
.
A quartic curve can have a maximum of:
- Four connected components
- Twenty-eight bi-tangentsBitangentIn mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
- Three ordinary double points.
Examples
- BicornBicornIn geometry, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne, is a rational quartic curve defined by the equationy^2=^2.It has two cusps and is symmetric about the y-axis.-History:...
curve - Bullet-nose curve
- Cartesian ovalCartesian ovalIn geometry, a Cartesian oval, named after René Descartes, is determined as follows. Let and be fixed points in the plane, and let and denote the Euclidean distances from these points to a third variable point . Let and be arbitrary real numbers. Then the Cartesian oval is the locus of...
- Cassini ovalCassini ovalA Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
- Deltoid curveDeltoid curveIn geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
- HippopedeHippopedeIn geometry, a hippopede is a plane curve determined by an equation of the form^2=cx^2+dy^2,...
- Lemniscate of BernoulliLemniscate of BernoulliIn geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
- Lemniscate of GeronoLemniscate of GeronoIn algebraic geometry, the lemniscate of Gerono, or lemnicate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero shaped like an \infty symbol, or figure eight...
- Lüroth quarticLüroth quarticIn mathematics, a Lüroth quartic is a nonsingular quartic plane curve containing the 10 vertices of a complete pentalateral. They were introduced by . showed that the Lüroth quartics form an open subset of a degree 54 hypersurface, called the Lüroth hypersurface, in the space P14 of all quartics...
- Klein quarticKlein quarticIn hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
- Spiric sectionSpiric sectionIn geometry, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve defined by equations of the form^2=dx^2+ey^2+f....
- Toric sectionToric sectionA toric section is an intersection of a plane with a torus, just as a conic section is the intersection of a plane with a cone.-Mathematical formulae:In general, toric sections are fourth-order plane curves of the form...
- Kampyle of Eudoxus

