
Bullet-nose curve
Encyclopedia
In mathematics
, a bullet-nose curve is a unicursal quartic curve
with three inflection point
s, given by the equation
The bullet curve has three double points in the real projective plane
, at x=0 and y=0, x=0 and z=0, and y=0 and z=0, and is therefore a unicursal (rational) curve of genus
zero.
If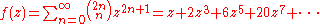
then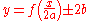
are the two branches of the bullet curve at the origin.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bullet-nose curve is a unicursal quartic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
with three inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s, given by the equation

The bullet curve has three double points in the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
, at x=0 and y=0, x=0 and z=0, and y=0 and z=0, and is therefore a unicursal (rational) curve of genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
zero.
If
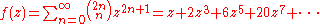
then
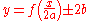
are the two branches of the bullet curve at the origin.

