
Lemniscate of Gerono
Encyclopedia
In algebraic geometry
, the lemniscate of Gerono, or lemnicate of Huygens, or figure-eight curve, is a plane algebraic curve
of degree four and genus
zero shaped like an
symbol, or figure eight. It has equation
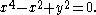
It was studied by Camille-Christophe Gerono
.
Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is

Another representation is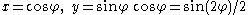
which reveals that this lemniscate is a special case of a lissajous figure.
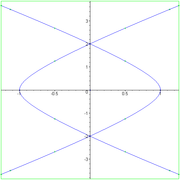
The dual curve
(see Plücker formula
), pictured below, has therefore a somewhat different character. Its equation is

Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the lemniscate of Gerono, or lemnicate of Huygens, or figure-eight curve, is a plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree four and genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
zero shaped like an
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
symbol, or figure eight. It has equation
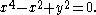
It was studied by Camille-Christophe Gerono
Camille-Christophe Gerono
Camille-Christophe Gerono was a French mathematician and co-editor of Nouvelles annales de mathématiques. He concerned himself above all with geometry. The Lemniscate of Gerono or figure-eight curve was named after him....
.
Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is

Another representation is
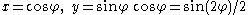
which reveals that this lemniscate is a special case of a lissajous figure.
The dual curve
Dual curve
In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree...
(see Plücker formula
Plücker formula
In mathematics, a Plücker formula, named after Julius Plücker, is one of a family of formulae, of a type first developed by Plücker in the 1830s, that relate certain numeric invariants of algebraic curves to corresponding invariants of their dual curves. The invariant called the genus, common to...
), pictured below, has therefore a somewhat different character. Its equation is



