Cartesian oval
Encyclopedia
In geometry
, a Cartesian oval
, named after René Descartes
, is determined as follows. Let and be fixed points in the plane, and let and denote the Euclidean distance
s from these points to a third variable point . Let and be arbitrary real number
s. Then the Cartesian oval is the locus
of points S satisfying . The two ovals formed by the four equations and are closely related; together they form a quartic plane curve
called the ovals of Descartes.
. When
it is a limaçon
of Pascal. If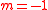
and 
the equation gives a branch of a hyperbola
and thus is not a closed oval.
where is the distance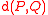
between the two fixed foci and , forms two ovals, the sets of points satisfying the two of the four equations
that have real solutions. The two ovals are generally disjoint, except in the case that or belongs to them. At least one of the two perpendiculars to through points and cuts this quartic curve in four real points; it follows from this that they are necessarily nested, with at least one of the two points and contained in the interiors of both of them. For a different parametrization and resulting quartic, see Lawrence.
design. By choosing the ratio of distances from and to match the ratio of sine
s in Snell's law
, and using the
surface of revolution
of one of these ovals, it is possible to design a so-called aplanatic lens, that has no spherical aberration
.
Additionally, if a spherical wavefront is refracted through a spherical lens, or reflected from a concave spherical surface, the refracted or reflected wavefront takes on the shape of a Cartesian oval. The caustic
formed by spherical aberration in this case may therefore be described as the evolute
of a Cartesian oval.
These curves were also studied by Newton
beginning in 1664. One method of drawing certain specific Cartesian ovals, already used by Descartes, is analogous to a standard construction of an ellipse
by stretched thread. If one stretches a thread from a pin at one focus to wrap around a pin at a second focus, and ties the free end of the thread to a pen, the path taken by the pen, when the thread is stretched tight, forms a Cartesian oval with a 2:1 ratio between the distances from the two foci. However, Newton rejected such constructions as insufficiently rigorous. He defined the oval as the solution to a differential equation
, constructed its subnormals
, and again investigated its optical properties.
The French mathematician Michel Chasles
discovered in the 19th century that, if a Cartesian oval is defined by two points and , then there is in general a third point on the same line such that the same oval is also defined by any pair of these three points.
James Clerk Maxwell
rediscovered these curves, generalized them to curves defined by keeping constant the weighted sum of distances from three or more foci, and presented a paper to the Royal Society of Edinburgh
on his results in 1846, at the young age of 15.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Cartesian oval
Oval
An oval is any curve resembling an egg or an ellipse, such as a Cassini oval. The term does not have a precise mathematical definition except in one area oval , but it may also refer to:* A sporting arena of oval shape** a cricket field...
, named after René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
, is determined as follows. Let and be fixed points in the plane, and let and denote the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
s from these points to a third variable point . Let and be arbitrary real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. Then the Cartesian oval is the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points S satisfying . The two ovals formed by the four equations and are closely related; together they form a quartic plane curve
Quartic plane curve
A quartic plane curve is a plane curve of the fourth degree. It can be defined by a quartic equation:Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0....
called the ovals of Descartes.
Special cases
In the equation , when and the resulting shape is an ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. When
it is a limaçonLimaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...
of Pascal. If
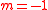and the equation gives a branch of a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
and thus is not a closed oval.
Polynomial equation
The set of points satisfying the quartic polynomial equation- ,
where is the distance
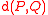between the two fixed foci and , forms two ovals, the sets of points satisfying the two of the four equations
- ,
that have real solutions. The two ovals are generally disjoint, except in the case that or belongs to them. At least one of the two perpendiculars to through points and cuts this quartic curve in four real points; it follows from this that they are necessarily nested, with at least one of the two points and contained in the interiors of both of them. For a different parametrization and resulting quartic, see Lawrence.
Applications in optics
As Descartes discovered, Cartesian ovals may be used in lensLens
-Optics:*Lens , an optical element which converges or diverges light**Lens , a part of the eye**Corrective lens for correction of human vision***Contact lens, placed on the cornea of the eye**Photographic lens, a lens designed for use on a camera...
design. By choosing the ratio of distances from and to match the ratio of sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
s in Snell's law
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
, and using the
surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
of one of these ovals, it is possible to design a so-called aplanatic lens, that has no spherical aberration
Spherical aberration
thumb|right|Spherical aberration. A perfect lens focuses all incoming rays to a point on the [[Optical axis|optic axis]]. A real lens with spherical surfaces suffers from spherical aberration: it focuses rays more tightly if they enter it far from the optic axis than if they enter closer to the...
.
Additionally, if a spherical wavefront is refracted through a spherical lens, or reflected from a concave spherical surface, the refracted or reflected wavefront takes on the shape of a Cartesian oval. The caustic
Caustic (optics)
In optics, a caustic or caustic network is the envelope of light rays reflected or refracted by a curved surface or object, or the projection of that envelope of rays on another surface. The caustic is a curve or surface to which each of the light rays is tangent, defining a boundary of an...
formed by spherical aberration in this case may therefore be described as the evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of a Cartesian oval.
History
The ovals of Descartes were first studied by René Descartes in 1637, in connection with their applications in optics.These curves were also studied by Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
beginning in 1664. One method of drawing certain specific Cartesian ovals, already used by Descartes, is analogous to a standard construction of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
by stretched thread. If one stretches a thread from a pin at one focus to wrap around a pin at a second focus, and ties the free end of the thread to a pen, the path taken by the pen, when the thread is stretched tight, forms a Cartesian oval with a 2:1 ratio between the distances from the two foci. However, Newton rejected such constructions as insufficiently rigorous. He defined the oval as the solution to a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, constructed its subnormals
Subtangent
In geometry, the subtangent and related terms are certain line segments defined using the line tangent to a curve at a given point and the coordinate axes...
, and again investigated its optical properties.
The French mathematician Michel Chasles
Michel Chasles
Michel Floréal Chasles was a French mathematician.He was born at Épernon in France and studied at the École Polytechnique in Paris under Siméon Denis Poisson. In the War of the Sixth Coalition he was drafted to fight in the defence of Paris in 1814...
discovered in the 19th century that, if a Cartesian oval is defined by two points and , then there is in general a third point on the same line such that the same oval is also defined by any pair of these three points.
James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
rediscovered these curves, generalized them to curves defined by keeping constant the weighted sum of distances from three or more foci, and presented a paper to the Royal Society of Edinburgh
Royal Society of Edinburgh
The Royal Society of Edinburgh is Scotland's national academy of science and letters. It is a registered charity, operating on a wholly independent and non-party-political basis and providing public benefit throughout Scotland...
on his results in 1846, at the young age of 15.